问题描述

多重背包问题是经典的动态规划问题之一，是 01 背包和完全背包的泛化：

给定 n 种物品和一个容量为 m 的背包。第 i 种物品的重量为 wei[i]，价值为 val[i]，并且数量有限，最多只能取 s[i] 件。

目标是在不超过背包容量的前提下，选择物品装入背包，使得总价值最大。

  • 与 01 背包的区别：01 背包中每种物品只有 1 件（s[i] = 1）。
  • 与完全背包的区别：完全背包中每种物品有无限件（s[i] = ∞）。
image-20251130195244607

问题分析

在学习了前两种背包的基础上，多重背包的问题还是很清晰的

可以看出，多重背包是介于 01 背包和完全背包之间的一种更通用的模型：

  • 当 s[i] = 1 时，退化为 01 背包
  • 当 s[i] 足够大（大于 m/wei[i]）时，退化为完全背包

那么，01 背包的状态转移 是这样的

1
2
// 01背包：对于第i件物品，选或不选
dp[i][j] = max(dp[i-1][j], dp[i-1][j-wei[i]] + val[i]);
  • 只有两种选择：不选第 i 件物品（继承 dp[i-1][j]），或选第 i 件物品（从 dp[i-1][j-wei[i]] 转移）。
  • 内层循环是逆序遍历容量，防止重复选取。

而01背包是否可以考虑成，每个物品数量只有一件的多重背包呢？

所以说，我们可以再扩展一维数组，用于表示枚举选择装入背包的该物品件数

前面我们学习了完全背包的决策优化，所以，物品（装得下）的件数肯定可以被转换成体积来枚举

所以可以得到这样的转移

1
2
3
4
5
// dp[i][j]前i件物品放入容量为j的背包的最大价值
// 多重背包：对于第i种物品，选0~s[i]件
for(int k = 0; k <= s[i] && k * wei[i] <= j; k++) {
    dp[i][j] = Math.max(dp[i][j], dp[i-1][j - k * wei[i]] + k * val[i]);
}

整体转移如下

1
2
3
4
5
6
7
8
9
10
// 物品
for(int i = 1; i <= n; i++) {
    // 体积
    for(int j = 0; j <= m; j++) {
        // 数量
        for(int k = 0; k <= s[i] && k * wei[i] <= j; k++) {
                    dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - k * wei[i]] + k * val[i]);
                }
            }
        }

分析完整的状态转移

  • 通用形式（多重背包）

    1
    2
    3
    4
    // dp[i][j] = max{ dp[i-1][j - k*wei[i]] + k*val[i] }，其中 0 ≤ k ≤ s[i] 且 k*wei[i] ≤ j
    for (int k = 0; k <= s[i] && k * wei[i] <= j; k++) {
        dp[i][j] = Math.max(dp[i][j], dp[i-1][j - k*wei[i]] + k*val[i]);
    }

  • 特殊情况 ：01 背包（s [i] = 1）

    1
    2
    3
    // 此时k只能取0或1，方程简化为：
    dp[i][j] = Math.max(dp[i-1][j],                  // k=0，不选
                        dp[i-1][j-wei[i]] + val[i]); // k=1，选1件

  • 特殊情况 ：完全背包（s [i] →+∞ ）

    1
    2
    3
    // 此时k可以取到j/wei[i]，方程可以优化为：
    dp[i][j] = Math.max(dp[i-1][j],                  // k=0，不选
                        dp[i][j-wei[i]] + val[i]);   // 选k件等价于先选k-1件再加1件

多重背包的边界条件与 01 背包、完全背包保持一致，因为它们共享相同的状态定义：

1
2
3
4
5
6
7
8
9
10
11
// dp[i][j] 表示前i种物品放入容量为j的背包的最大价值

// 初始条件1：没有物品时（i=0），无论容量多少，价值都是0
for (int j = 0; j <= m; j++) {
    dp[0][j] = 0;
}

// 初始条件2：容量为0时（j=0），无论有多少物品，价值都是0
for (int i = 0; i <= n; i++) {
    dp[i][0] = 0;
}

时间复杂度分析

  • 状态总数：O(n × m)，其中n是物品种类数，m是背包容量。
  • 每个状态的计算量：对于每个状态dp[i][j]，需要枚举k从 0 到s[i]（最多j/wei[i]次），即O(s_max)，其中s_max是物品的最大数量。
  • 总时间复杂度：O(n × m × s_max)。

空间复杂度

  • 二维数组实现：O(n × m)，需要存储整个状态表。

很明显，这完全可以优化

滚动数组与决策优化

首先，和前面的01背包和完全背包一样，第一优化的思路是滚动数组与决策优化，来省下空间和时间

在朴素解法中，我们使用二维数组 dp[i][j] 表示前 i 种物品、容量为 j 时的最大价值。观察状态转移方程：

1
dp[i][j] = max(dp[i][j], dp[i-1][j - k*wei[i]] + k*val[i]);

和 01背包 一样，可以发现，计算 dp[i][j] 时只依赖于上一层（i-1）的状态，而与更早的层（i-2, i-3…）无关。因此，我们可以用一维数组来复用存储空间。

那么此时，状态变量可以这样定义

1
int[] dp = new int[m + 1];

此时 dp[j] 表示：处理到当前物品时，容量为 j 的背包能装的最大价值。

那么多重背包是否也应该进行逆序遍历容量，和01背包一样，多重背包在滚动掉一维之后也需要进行逆序枚举

如果正序遍历（如完全背包），会导致同一物品被多次选取（因为 dp[j - wei[i]] 已经是本轮更新后的值，你正序遍历会把之前的状态再选择一次）

1
for(int j = m; j >= wei[i]; j--) { // 逆序枚举容量

那么决策优化如何优化呢？

从数量下手，枚举数量的边界条件是k <= s[i] && k * wei[i] <= j，这是双重限制：

  • k <= s[i]：不超过物品的数量上限。
  • k * wei[i] <= j：不超过当前背包容量。

实际上，我在上面写的时候，应该是用三维数组的，因为上面的代码我在想的时候就把完全背包的体积枚举也写进去了

那么状态转移如下

对于每个容量 j，我们比较两种选择：

  • 不选当前物品：保持 dp[j] 不变（即上一轮的最优值）。
  • 选 k 件当前物品：用 dp[j - k*wei[i]] + k*val[i] 更新 dp[j]。

时间复杂度仍为 O(n×m×s_max)。空间复杂度是O(m)

当物品数量 s[i] 很大时（如 1000），效率依然不高。此时可以用二进制拆分优化

二进制拆分

二进制拆分就是把 “数量有限的物品” 转化为 “若干组 01 背包物品”，从而将时间复杂度从 O(n×m×s_max) 降到 O(n×m×log s_max)。

朴素解法的问题在于：当物品数量 s[i] 很大时（比如 s[i]=1000），内层枚举 k 的循环会执行 1000 次，时间效率极低。

二进制拆分的核心思路是：用少量 “组合物品” 覆盖 0~s [i] 的所有选取数量，把多重背包转化为 01 背包求解，大幅减少枚举次数。

image-20251130201500478

二进制拆分的数学原理是这样的

对于任意整数 s（物品数量），可以拆分为若干个形如 2^0, 2^1, 2^2, ..., 2^k, r 的数（其中 r = s - (2^(k+1)-1)，且 0 < r < 2^(k+1)），这些数的组合可以表示 0~s 之间的任意整数。

比如：

  • s=12：拆分为 1(2^0)、2(2^1)、4(2^2)、5(剩余)，1+2+4+5=12，且 1~12 的任意数都能由这几个数组合得到（如 3=1+2、7=1+2+4、12=1+2+4+5）；
  • s=50：拆分为 1、2、4、8、16、19，1+2+4+8+16=31，剩余 19，31+19=50，0~50 的任意数都能组合出来。

这样拆分就快了很多，因为少枚举的东西少了很多，比如当s[i]=1000时：

  • 朴素解法需要枚举 1000 次；
  • 二进制拆分只需枚举log2(1000)≈10次，效率提升 100 倍。

那么如何拆分呢

先定义这样的一些量

1
2
3
4
5
6
7
static final int N = 2005; // 背包容量上限
static int n, m;           // n=物品种类数，m=背包容量
static int wei1, val1, s;  // 临时存储单个物品的重量、价值、数量
// wei/val：存储拆分后的所有“组合物品”的重量/价值（N*12是因为log2(2000)≈11，足够覆盖）
static int[] wei = new int[N * 12];
static int[] val = new int[N * 12];
static int[] f = new int[N]; // 滚动数组，存储01背包的dp值

二进制拆分每一种物品的代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int num = 1; // 拆分后物品的计数（从1开始，对应01背包的物品编号）
for (int i = 1; i <= n; i++) {
    wei1 = scanner.nextInt(); // 读入第i种物品的重量
    val1 = scanner.nextInt(); // 读入第i种物品的价值
    s = scanner.nextInt();    // 读入第i种物品的数量
    
    // 核心：按2的幂次拆分
    for (int j = 1; j <= s; j <<= 1) {
        wei[num] = j * wei1;  // 组合物品的重量 = 拆分系数 × 原重量
        val[num++] = j * val1;// 组合物品的价值 = 拆分系数 × 原价值
        s -= j;               // 剩余数量减少
    }
    // 处理剩余不足2^k的部分
    if (s > 0) {
        wei[num] = s * wei1;
        val[num++] = s * val1;
    }
}

也就是说，每个物品的重量和价值每次 *2 拆分，不足的直接单开

那么这样，问题和上面转换成 01背包 的了，因为此时的wei[i]和val[i]都是拆分后的 “组合物品”，每个转换后的物品都只有一件，所以只能选一次

1
2
3
4
5
6
7
8
// 枚举拆分后的所有物品（01背包）
for (int i = 1; i < num; i++) {
    // 逆序遍历容量（01背包核心，防止重复选取）
    for (int j = m; j >= wei[i]; j--) {
        f[j] = Math.max(f[j], f[j - wei[i]] + val[i]);
    }
}
System.out.println(f[m]);
  • 注意逆序遍历容量：保证每个组合物品只被选一次，和之前的 01 背包滚动数组逻辑完全一致；

单调队列优化

思路如何转到使用单调队列优化

二进制优化通过将物品拆分为 log(s) 个二进制组合，转化为 01 背包问题，但时间复杂度仍为 O(nW log s)。而单调队列优化能将时间复杂度降至 O(nW)，效率更高。

首先，我们还是使用一维空间优化的定义： f[i] 代表容量不超过 i 时的最大价值。

这样，多重背包的状态转移方程为：

1
f[k] = max{ f[k - x*w] + x*v }  （其中 x 为选取数量，0 ≤ x ≤ min(s, k/w)）
  • 即对于容量 k，最优解是从「不选当前物品」「选 1 个」…「选 s 个」中取最大值。

在朴素的多重背包解决方案中，当我们在处理某一个物品从 f[0] 到 f[C] 的状态时，每次都是通过遍历当前容量 x 能够装多少件该物品，然后从所有遍历结果中取最优。

但事实上，转移只会发生在「对当前物品体积取余相同」的状态之间。

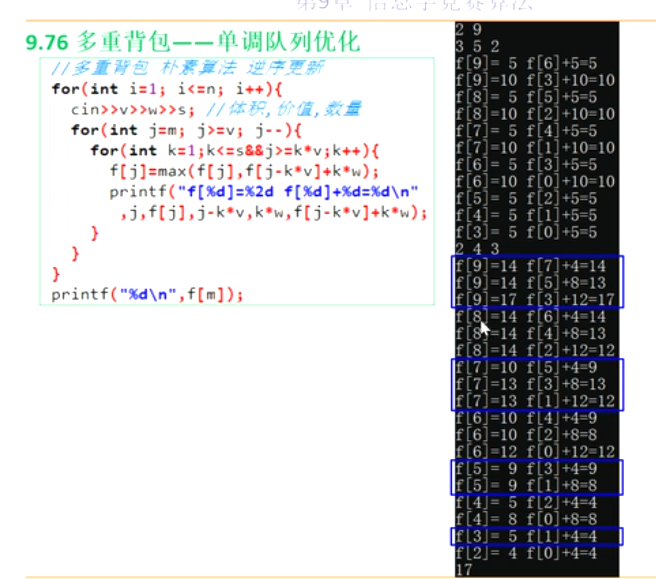
image-20251130202454088

可以发现，取余相同的物品可以被划分为一组，例如，f[6]可以通过f[4]，f[2]，f[0]来更新

观察发现，对于同一物品，容量 k 与 k + w 仅差一个物品的重量。因此可以按 k mod w 分组（共 w 组），每组内的容量满足 k = j + t*w（j 为余数，t 为非负整数）。

  • 例如，w=3 时，余数 j=0 的组包含 0,3,6,9...，j=1 的组包含 1,4,7,10... 等。

同一组内的状态转移只与组内元素相关，因为增加物品数量只会在组内移动（每次加 w）。

所以，可以这样总结，f是按照类更新的，那么可以把 f[0] 到 f[m]的按照体积 v 的余数拆分成 v 个类

image-20251130203019702

可以引入滑动窗口的最值问题了，对每组 的余数j，设 t = k/w（即 k = j + t*w），转移方程可改写为：

1
f[j + t*w] = max{ g[j + (t - x)*w] + x*v }  （0 ≤ x ≤ min(s, t)）

其中 g 是上一轮的 f 数组（备份，避免覆盖）。

令 t' = t - x，则 x = t - t'，方程变为：

1
f[j + t*w] = max{ g[j + t'*w] - t'*v } + t*v  （t' ≥ t - s 且 t' ≤ t）

此时，max{...} 部分是关于 t' 的滑动窗口（窗口大小为 s+1），可以用单调队列维护窗口内的最大值，从而将每组的更新时间从 O(W/w * s) 降至 O(W/w)。

单调队列优化背后详细的数学推导

很多人卡在这里是因为不理解为什么要构造 g[j + t' * w] - t'* v 这样一个奇怪的数值放入队列。

老实说，我也不是很清晰

首先，回顾一下，对于体积为 w，价值为 v 的物品。

当我们计算 f[j] 时，只能由 f[j − w], f[j − 2w]… 转移而来。

  • f[5] 的值只可能来自 f[5], f[5 − w], f[5 − 2w]…
  • f[4] 的值只可能来自 f[4], f[4 − w], f[4 − 2w]…

f[5] 和 f[4] 之间在当前这一轮物品的计算中是老死不相往来的。

对于按余数 j 分组的情况（0 ≤ j < w，w 为物品重量），组内的容量满足： k = j + t × w 所以，我们才把整个背包容量 W 按照 对 w 取模的余数 r (0 ≤ r < w) 分成 w 组。

接下来，我们只盯着其中一组看。假设这一组的容量序列是，事实上，每一组都能被以下列的形式拆分 r, r + w, r + 2w, r + 3w, …, r + t ⋅ w, … 为了方便书写，我们把这一组的状态单独拿出来，定义为一个简单的数组 G

  • 令 G[t] = g[r + t ⋅ w] （g 是上一轮的 DP 状态，即还没放入当前物品时的状态）。

假设我们现在要计算 当前容量 下的最大价值。

设当前容量为 j = r + t ⋅ w。我们最多能选 s 个物品。

所以，按照我们上面的推导，我们可以选 x 个物品 (0 ≤ x ≤ s)。 f[j] = max {g[j − x ⋅ w] + x ⋅ v} 我们要把这个方程里的下标换成 t（组内编号）：

  • 当前容量下标对应 t。
  • 前面某个容量下标对应 t′ = t − x，即选了 x 个物品后剩下的空间对应的下标。也就是，选取 x 个物品后，前一个状态的容量是 $ k - x w = j + (t - x) w，对应组内编号t’ = t - x$
  • 因为 x = t − t′，所以选的物品数量就是 (t − t′)。等于当前组内编号 t 与前一个状态组内编号 t′ 的差，这是必然的
    • t 表示 “当前容量比基础余数 j 多了 t 个 w”，即总空间可以容纳 t 个该物品（理论上，不考虑数量限制 s）。
    • t′ 表示 “前一个状态的容量比基础余数 j 多了t′ 个 w”，即前一个状态已经用了t′ 个 w 的空间。
    • 两者的差 t − t′ 就是 “从 t′ 到 t 新增的空间”，恰好等于新增的物品数量 x（每个物品占 w 空间）。

代入公式： f[r + t ⋅ w] = max {g[r + t′ ⋅ w] + (t − t′) ⋅ v} 这里的限制条件是：

  1. x ≤ s ⟹ t − t′ ≤ s ⟹ t′ ≥ t − s （不能回头太远）
  2. x ≥ 0 ⟹ t′ ≤ t （不能超过当前位置）

所以，t′ 的范围是 [t − s, t]。这是一个长度为 s + 1 的滑动窗口。

接下来进行变形，因为这个不太方便计算

看这个式子： max {g[r + t′ ⋅ w] + (t − t′) ⋅ v} 我们要针对 t′ 找最大值。请注意式子里的项：

  • g[r + t′ ⋅ w]：只和 t′ 有关。
  • t ⋅ v：只和 t（当前位置）有关，对于 t′ 的遍历来说，它是常数。
  • −t′ ⋅ v：只和 t′ 有关。

我们可以把常数项 t ⋅ v 提到 max 外面：

f[r + t ⋅ w] = max {g[r + t′ ⋅ w] − t′ ⋅ v} + t ⋅ v 这就是需要的那个公式。

那么其实还存在一个问题，就是公式内max {g[r + t′ ⋅ w] − t′ ⋅ v}中，为什么要减去 t′ ⋅ v？这有什么物理意义？

原始公式的物理意义是：

当前容量 (r + t ⋅ w)的最大价值 = 所有合法前序容量(r + t′ ⋅ w)的价值中的最大值 + 新增物品的价值

单调队列的核心作用是 维护一个滑动窗口内的 “最值”，且这个 “最值” 必须只和 “窗口内的元素本身” 有关，和 “当前窗口的位置” 无关。

原始公式内max {g[r + t′ ⋅ w] + (t − t′) ⋅ v}展开后发现g[r + t′ ⋅ w] + t ⋅ v − t′ ⋅ v​，它被包含在 max 里面，导致：

  • 每次计算 max 时，都要带着这个随 t 变化的常数；
  • 单调队列无法提前维护 “窗口内元素的固定最值”—— 因为这个常数会让每个 t 对应的 “比较基准” 都不一样。

所以我们才需要把 随 t 变化的项$ t v$ 从 max 里面剥离出来 g[r + t′ ⋅ w] + (t − t′) ⋅ v = (g[r + t′ ⋅ w] − t′ ⋅ v) + t ⋅ v 因为 t ⋅ v 对同一个 t 的所有 t′ 都是常数，所以可以提到 max 外面，得到： f[r + t ⋅ w] = max {g[r + t′ ⋅ w] − t′ ⋅ v} + t ⋅ v 这意味着：对于滑动窗口内的所有 t′，我们可以提前计算出这个值，用单调队列维护它的最大值 —— 当 t 滑动时，只需取出队列中的最大值，再加上当前的 t ⋅ v，就能得到当前状态的最大价值。

现在公式变成了：F[t] = max {Val(t′)} + t ⋅ v

Val(t′) 的数值一旦算出来，就不会随着滑动窗口的移动而改变了。这正是单调队列能够维护的前提！

那么，该单调队列就这样维护和操作，队列里存放的是下标 k。

在这个队列里，我们要维护 Val(k) = g[r + k ⋅ w] − k ⋅ v 是单调递减的。

对于分组中的每一个位置 t（从 0 到 最大）：

  1. 计算当前 t 的潜力值： temp = g[r + t ⋅ w] − t ⋅ v。

  2. 入队维护单调性： 如果队列不空，且队尾元素的潜力值  ≤ temp，说明队尾那个 t′ 虽然位置靠后，但潜力太差，甚至不如现在的 t（t 更靠后且潜力大，肯定更优）。 扔掉队尾，直到队尾潜力值  > temp。 将 t 入队。

  3. 出队维护窗口大小： 如果队头元素的下标 qhead < t − s（说明这个最优解太远了，超过了物品数量限制 s），扔掉队头。

  4. 计算当前 f： 队头就是当前窗口内 Val 最大的下标 best。 f[r + t ⋅ w] = (Val(best)) + t ⋅ v 即： f[r + t ⋅ w] = (g[r + best ⋅ w] − best ⋅ v) + t ⋅ v

最后我们举个栗子

设 W = 10, w = 2, v = 4, s = 2（每件体积2，价值4，最多2件）。

按 j (mod  2) 分组，我们看 r = 0 这一组：0, 2, 4, 6, 8, 10。

假设上一轮的 g​ 数组（部分）如下： g[0] = 0, g[2] = 3, g[4] = 5, g[6] = 15, g[8] = 15, g[10] = 20 (注：这些数是我编的，为了演示)

对应的组内下标 t:

  • t = 0→ 真实容量 0
  • t = 1→ 真实容量 2
  • t = 2→ 真实容量 4
  • …

计算 Val(t) = g[t] − t ⋅ v：

  • t = 0 : Val = 0 − 0 * 4 = 0
  • t = 1 : Val = 3 − 1 * 4 = −1
  • t = 2 : Val = 5 − 2 * 4 = −3
  • t = 3 : Val = 15 − 3 * 4 = 3

开始滑动窗口 (窗口大小 s = 2)：

  1. t = 0:
    • 入队：Val(0) = 0。队列：[0]
    • 计算 f[0]：队头是0。MaxVal = 0。
    • f[0] = 0 + 0 * 4 = 0。
  2. t = 1:
    • 入队：Val(1) = −1。比队尾0小，直接入。队列：[0, 1]
    • 检查过期：0 ≥ 1 − 2，没过期。
    • 计算 f[2]：队头是0 (Val = 0)。
    • f[2] = 0 + 1 * 4 = 4。（即：从0开始，拿1个）
  3. t = 2:
    • 入队：Val(2) = −3。比队尾-1小，直接入。队列：[0, 1, 2]
    • 检查过期：0 ≥ 2 − 2，没过期。
    • 计算 f[4]：队头是0 (Val = 0)。
    • f[4] = 0 + 2 * 4 = 8。（即：从0开始，拿2个）
  4. t = 3:
    • 入队：Val(3) = 3。
      • 队尾是2 (Val = −3)，3 > -3，弹出2。
      • 队尾是1 (Val = −1)，3 > -1，弹出1。
      • 队尾是0 (Val = 0)，3 > 0，弹出0。
      • 放入3。队列：[3]
    • 检查过期：队头3，当前3。3 ≥ 3 − 2，没过期。
    • 计算 f[6]：队头是3 (Val = 3)。
    • f[6] = 3 + 3 * 4 = 15。（注意这里！它选择了保留原来的 g[6] = 15，也就是一个都不拿，因为 g[6] 实在太大了，比从 f[2] 或 f[4] 转移过来都大）。

模板代码

朴素实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
// 多重背包
// 第i种物品可以取0到si件
// 转换为01背包求解

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        int m = scanner.nextInt();
        int[] val = new int[n + 1];
        int[] wei = new int[n + 1];
        int[] s = new int[n + 1];  // 数量
        // 最大价值是dp[i][j]前i件物品放入容量为j的背包的最大价值的函数关系
        int[][] dp = new int[210][210];

        for (int i = 1; i <= n; i++) {
            // 费用,价值,数量
            val[i] = scanner.nextInt();
            wei[i] = scanner.nextInt();
            s[i] = scanner.nextInt();
        }

        // 物品
        for(int i = 1; i <= n; i++) {
            // 体积
            for(int j = 0; j <= m; j++) {
                // 数量
                for(int k = 0; k <= s[i] && k * wei[i] <= j; k++) {
                    dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - k * wei[i]] + k * val[i]);
                }
            }
        }

        System.out.println(dp[n][m]);

        scanner.close();
    }
}

滚动数组与决策优化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        int m = scanner.nextInt();
        int[] val = new int[n + 1];
        int[] wei = new int[n + 1];
        int[] s = new int[n + 1];  // 数量

        int[] dp = new int[210];

        for (int i = 1; i <= n; i++) {
            // 费用,价值,数量
            val[i] = scanner.nextInt();
            wei[i] = scanner.nextInt();
            s[i] = scanner.nextInt();
        }

        // 物品
        for(int i = 1; i <= n; i++) {
            // 体积，这里需要逆序枚举，因为是后更新
            for(int j = m; j >= wei[i]; j--) {
                // 数量，同时注意体积不能超
                for(int k = 0; k <= s[i] && k * wei[i] <= j; k++) {
                    // 滚动数组优化
                   dp[j] = Math.max(dp[j], dp[j - k * wei[i]] + k * val[i]);
                }
            }
        }

        System.out.println(dp[m]);

        scanner.close();
    }
}

二进制拆分

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
import java.util.Scanner;

// 二进制拆分就是用先准备2^k拆分然后组合成任意大小的数
// 可以把多重背包优化成01背包

// 将第i种物品拆分成若干种，每件物品的体积和价值乘一个拆分系数，就可以转化成01背包的物品求解

public class Main {
    static final int N = 2005; // 2000 < 2^12
    static int n, m;
    static int wei1, val1, s;
    static int[] wei = new int[N * 12];
    static int[] val = new int[N * 12];
    static int[] f = new int[N];

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        n = scanner.nextInt();
        m = scanner.nextInt();

        // 二进制拆分
        int num = 1;    // 拆分计数
        for (int i = 1; i <= n; i++) {
            // 体积，价值，数量
            wei1 = scanner.nextInt();
            val1 = scanner.nextInt();
            s = scanner.nextInt();
            // 把本来存每一件物品，变成存j件的，然后j每次*2，这样处理相当于每个位置都是下一个位置的2倍
            for (int j = 1; j <= s; j <<= 1) {
                wei[num] = j * wei1;
                val[num++] = j * val1;
                s -= j;
            }
            // 处理剩余的
            if (s > 0) {
                wei[num] = s * wei1;
                val[num++] = s * val1;
            }
        }

        // 01背包
        // 物品数循环到小于num，拆分后拆成了num个
        for (int i = 1; i < num; i++) {
            // 逆序枚举
            for (int j = m; j >= wei[i]; j--) {
                f[j] = Math.max(f[j], f[j - wei[i]] + val[i]);
            }
        }

        System.out.println(f[m]);

        scanner.close();
    }
}

单调队列优化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
import java.util.Scanner;

// dp数组是按类更新的，可以按照f[0..m]按体积v的余数拆分成v个类
// f[j]  f[j+v]  f[j+2v]....f[j+kv]   其中j是v的余数，0<=j<=v-1
// 可以看出每一类中的差是v的整数倍（放物品总数一个个放）
// f[j]就是由前面不超过数量s的同类值递推得到的，这就相当于从前面宽度为s的窗口挑选最大值来更新当前值
// 所以，用单调队列来维护最大值，从而把更新f[j]的次数缩减为1次

public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        // 种类n,容量W
        int n = scanner.nextInt();
        int W = scanner.nextInt();
        final int N = 40005;
        int[] q = new int[N];
        int[] f = new int[N];    // f[k] = 窗口中的最大价值 + 还能放入物品的价值
        int[] g = new int[N];   // 备份f的数组


        while (n-- > 0) {
            System.arraycopy(f, 0, g, 0, f.length);  // 备份f数组到g
            int v = scanner.nextInt(); // 物品价值
            int w = scanner.nextInt(); // 物品重量
            int s = scanner.nextInt(); // 物品数量

            // 枚举余数w(w个类)
            for (int j = 0; j < w; j++) {
                int h = 1, t = 0; // 单调队列的头和尾
                // 对每个类使用单调队列
                // 对于每个余数 j，枚举所有 k = j,j+w,j+2w（同类中枚举）
                for (int k = j; k <= W; k += w) {
                    // q[h]不在窗口[k-s*w, k-w]内，维护单调队列，移除超出范围的元素
                    // 因为在背包容量 k 的限制下，减去最多能选的s个物品乘重量为左边界，当然右边界就是选择 1 个当前物品
                    if (h <= t && q[h] < k - s * w) h++;
                    // 窗口是在g数组上滑动的
                    // (k - q[t]) / w是从状态 q[t] 到状态 k 还可以放入多少个当前物品
                    // 如果新值g[k]比队尾g[q[t]]状态更优，转换过去
                    while (h <= t && g[k] >= g[q[t]] + (k - q[t]) / w * v) t--;
                    q[++t] = k;   // 队头出队
                    // f[k] = 窗口中的最大价值 + 还能放入物品的价值
                    f[k] = g[q[h]] + (k - q[h]) / w * v; // 更新f[k]

                }
            }
        }

        System.out.println(f[W]); // 输出最大价值
        scanner.close();
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
// 单调队列 O(n*W)
#include<bits/stdc++.h>
using namespace std;

const int N=40010;
int n,W,w,v,m,q[N];
int f[N],g[N];

int main(){
  scanf("%d%d",&n,&W);        //种类n,容量W
  while(n--){
    memcpy(g,f,sizeof(f));    //f备份
    scanf("%d%d%d",&v,&w,&m); //价值,重量,数量
    
    for(int j=0; j<w; j++){   //0,1,2...w-1个类
      int h=1,t=0;
      for(int k=j; k<=W; k+=w){ //0,w,2w,3w...
        while(h<=t && q[h]<k-m*w) h++; //[k-m*w...k-w],k
        while(h<=t && g[k]>=g[q[t]]+(k-q[t])/w*v) t--; //q[t]...k
        q[++t]=k;
        f[k]=g[q[h]]+(k-q[h])/w*v; //q[h]...k
      }
    }
  }
  printf("%d\n",f[W]);
}

例题

问题

[P1782 旅行商的背包][https://www.luogu.com.cn/problem/P1782]

P1782 旅行商的背包

题目描述

小 S 坚信任何问题都可以在多项式时间内解决，于是他准备亲自去当一回旅行商。在出发之前，他购进了一些物品。这些物品共有 n 种，第 i 种体积为 Vi，价值为 Wi，共有 Di 件。他的背包体积是 C。怎样装才能获得尽量多的收益呢？作为一名大神犇，他轻而易举的解决了这个问题。

然而，就在他出发前，他又收到了一批奇货。这些货共有 m 件，第 i 件的价值 Yi 与分配的体积 Xi 之间的关系为：Yi = aiXi2 + biXi + ci。这是件好事，但小 S 却不知道怎么处理了，于是他找到了一位超级神犇（也就是你），请你帮他解决这个问题。

输入格式

第一行三个数 n, m, C，如题中所述；

以下 n 行，每行有三个数 Vi, Wi, Di，如题中所述；

以下 m 行，每行有三个数 ai, bi, ci，如题中所述。

输出格式

仅一行，为最大的价值。

输入输出样例 #1

输入 #1

1
2
3
4
2 1 10
1 2 3
3 4 1
-1 8 -16

输出 #1

1
10

说明/提示

样例解释

前两种物品全部选走，最后一个奇货分给 4 的体积，收益为2 × 3 + 4 × 1 + (−1) × 16 + 8 × 4 + (−16) = 10。

限制与约定

对于 100% 的数据，1 ≤ n ≤ 104，1 ≤ m ≤ 5，1 ≤ C ≤ 104，$ 1 W_i,V_i,D_i ，-1000 a_i,b_i,c_i $。

问题分析

这道题目将多重背包问题（Multiple Knapsack）与分组背包（Group Knapsack/泛化物品）结合在了一起。

这个 N 来说是较大的了，有104，而且如何合并特殊的二次函数物品。

题目明显分为两个部分，我们需要在同一个背包容量 C 下解决：

  • 标准的多重背包
    • 这些物品共有 n 种，第 i 种体积为 Vi，价值为 Wi，共有 Di 件，如果使用朴素拆分（当做 0/1 背包），复杂度是 O(C ⋅ ∑Di)，会超时。二进制拆分复杂度为 O(C ⋅ n ⋅ logD)，计算量约为 109，在 Java 中非常危险，容易 TLE。因此，我们需要单调队列优化。
  • 奇货（二次函数物品）
    • 奇货共有 m 件，第 i 件的价值 Yi 与分配的体积 Xi 之间的关系为：Yi = aiXi2 + biXi + ci。
    • m 非常小
    • 这可以看作分组背包。对于每一个“奇货”，我们可以选择分配 0, 1, 2, …, C 的体积给它。这就相当于一组互斥的物品，我们只能从中选一种“分配方案”。

所以，总体考虑这样的策略

  • 先处理 n 种普通物品，使用单调队列优化的多重背包算法，得到数组 dp[0…C]，其中 dp[j] 表示仅使用普通物品、容量为 j 时的最大价值。
  • 再处理 m 个奇货。对于每个奇货，我们遍历背包容量 j（从 C 到 0），尝试枚举分配给该奇货的体积 k（从 0 到 j），更新 DP 数组。

那么多重背包考虑单调队列优化

先列出朴素情况下的状态转移方程 dp[j] = max {dp[j − k ⋅ Vi] + k ⋅ Wi}  (0 ≤ k ≤ Di) 假设当前处理物品重量为 v，价值为 w，数量为 d。 我们将背包容量 j 按照模 v 的余数 r 分组：j = q ⋅ v + r。 对于固定的余数 r，方程变为： $$ dp[q \cdot v + r] = \max_{\substack{0 \leq k \leq d}} \left\{ dp\left[(q - k) \cdot v + r\right] + k \cdot w \right\} $$ 令 t = q − k，则 q − d ≤ t ≤ q。代入k = q − t，这样就让单调队列内的非单调项消去了 dp[q ⋅ v + r] = max {dp[t ⋅ v + r] + (q − t) ⋅ w} 移项提取常数 q ⋅ w： dp[q ⋅ v + r] = max {dp[t ⋅ v + r] − t ⋅ w} + q ⋅ w 这样就推到成了我们需要在一个长度为 d 的滑动窗口 [q − d, q] 内，找到 dp[t ⋅ v + r] − t ⋅ w 的最大值。

处理完所有普通物品后，我们得到了基础的 dp 数组。 对于第 i 个奇货（参数 a,b,c）：

  • 它实际上是一个包含 C+1 种选择的物品组：

    • 选择 1：体积 0，价值 0（不选）
    • 选择 2：体积 1，价值 a(1)2 + b(1) + c
    • …
    • 选择 C：体积 C，价值 a(C)2 + b(C) + c

  • 我们倒序遍历背包容量 j（从 C 到 0），再遍历分配给该奇货的体积 k（从 0 到 j）： dp[j] = max (dp[j], dp[j − k] + (a ⋅ k2 + b ⋅ k + c)) 题目隐含若不选该物品则价值为0，按若分配体积 k≥1 则按公式计算。若 k=0 代入公式价值大于0，通常也视为一种可选方案

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
//package 动态规划.subject.背包.P1782_旅行商的背包;

import java.io.*;
import java.util.*;

public class Main {
    static int MAX_C = 10005;
    static int[] dp = new int[MAX_C];
    static int[] preDp = new int[MAX_C];
    static int[] q = new int[MAX_C];

    static int n, m, C;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StreamTokenizer st = new StreamTokenizer(br);

        st.nextToken(); n = (int) st.nval;
        st.nextToken(); m = (int) st.nval;
        st.nextToken(); C = (int) st.nval;

        // --- 多重背包 ---
        for (int i = 0; i < n; i++) {
            st.nextToken(); int v = (int) st.nval;
            st.nextToken(); int w = (int) st.nval;
            st.nextToken(); int d = (int) st.nval;

            if (v == 0) continue;
            mqPack(v, w, d);
        }

        // --- 奇货处理 ---
        for (int i = 0; i < m; i++) {
            st.nextToken(); int a = (int) st.nval;
            st.nextToken(); int b = (int) st.nval;
            st.nextToken(); int c = (int) st.nval;

            // 备份当前状态，避免重复使用
            System.arraycopy(dp, 0, preDp, 0, C + 1);

            // 从大到小遍历
            for (int j = 0; j <= C; j++) {
                // 尝试分配 k 体积给这个奇货
                for (int k = 0; k <= j; k++) {
                    int val = a * k * k + b * k + c;
                    dp[j] = Math.max(dp[j], preDp[j - k] + val);
                }
            }
        }

        System.out.println(dp[C]);
    }

    private static void mqPack(int v, int w, int d) {
        System.arraycopy(dp, 0, preDp, 0, C + 1);

        for(int r = 0; r < v; r++){
            int head = 0, tail = -1;

            for(int k = 0; k * v + r <= C; k++){
                int val = preDp[k * v + r] - k * w;

                // 维护单调递减队列
                while(head <= tail && val >= preDp[q[tail] * v + r] - q[tail] * w){
                    tail--;
                }

                tail++;
                q[tail] = k;

                // 移除滑出窗口的元素
                while(head <= tail && q[head] < k - d){
                    head++;
                }

                int bK = q[head];
                dp[k * v + r] = (preDp[bK * v + r] - bK * w) + k * w;
            }
        }
    }
}
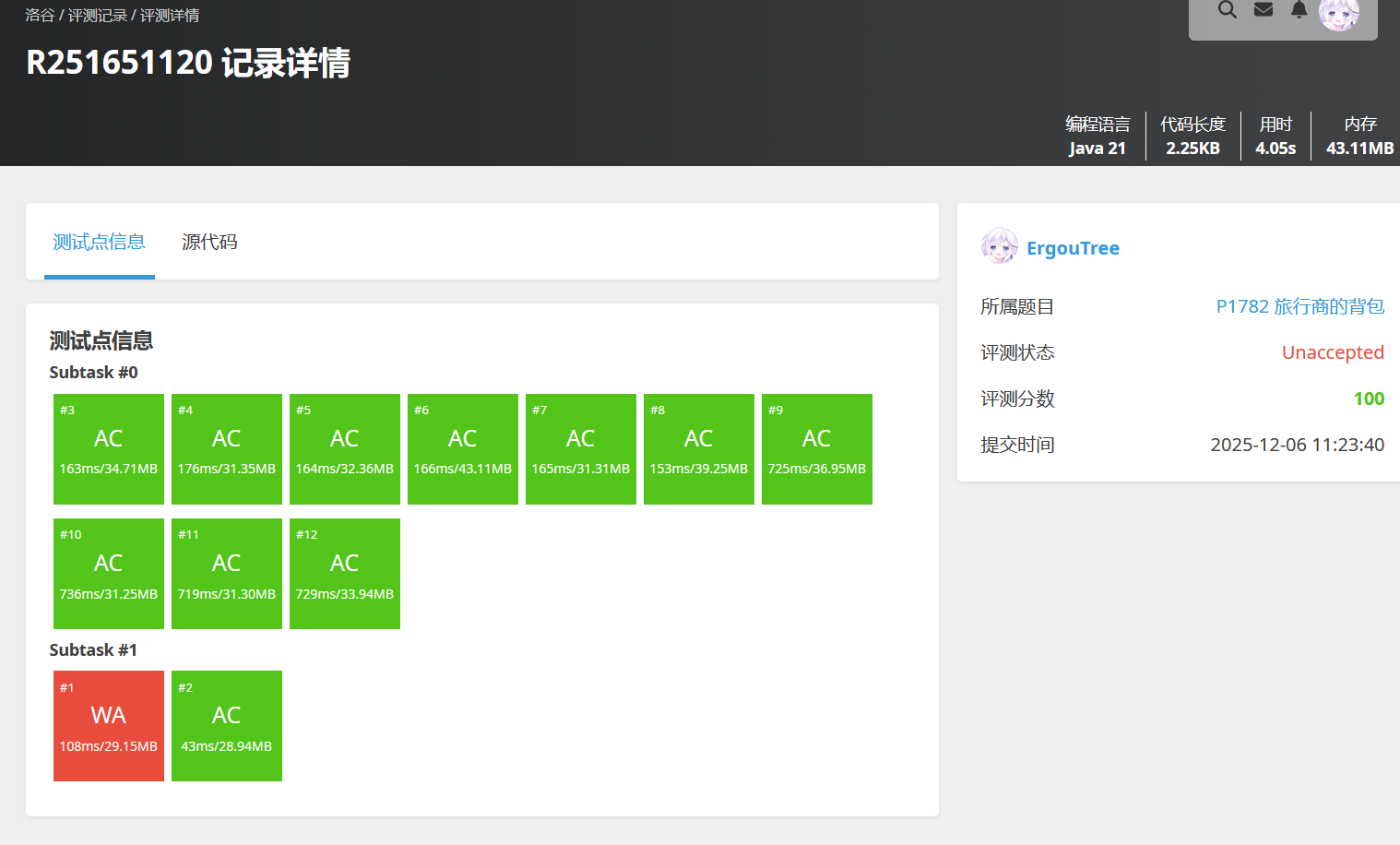
image-20251206112342207

这是什么情况呢？

忘记开long了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
import java.io.*;
import java.util.*;

public class Main {
    static int MAX_C = 10005;
    static long[] dp = new long[MAX_C];
    static long[] preDp = new long[MAX_C];
    static int[] q = new int[MAX_C];

    static int n, m, C;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StreamTokenizer st = new StreamTokenizer(br);

        st.nextToken(); n = (int) st.nval;
        st.nextToken(); m = (int) st.nval;
        st.nextToken(); C = (int) st.nval;

        // --- 多重背包 ---
        for (int i = 0; i < n; i++) {
            st.nextToken(); int v = (int) st.nval;
            st.nextToken(); int w = (int) st.nval;
            st.nextToken(); int d = (int) st.nval;

            if (v == 0) continue;
            mqPack(v, w, d);
        }

        // --- 奇货处理 ---
        for (int i = 0; i < m; i++) {
            st.nextToken(); int a = (int) st.nval;
            st.nextToken(); int b = (int) st.nval;
            st.nextToken(); int c = (int) st.nval;

            // 备份当前状态，避免重复使用
            System.arraycopy(dp, 0, preDp, 0, C + 1);

            for (int j = C; j >= 0; j--) {
                // 尝试分配 k 体积给这个奇货
                for (int k = 0; k <= j; k++) {
                    long val = (long)a * k * k + (long)b * k + c;
                    if (val > 0) {
                        dp[j] = Math.max(dp[j], preDp[j - k] + val);
                    }
                }
            }
        }

        System.out.println(dp[C]);
    }

    private static void mqPack(int v, int w, int d) {
        System.arraycopy(dp, 0, preDp, 0, C + 1);

        for(int r = 0; r < v; r++){
            int head = 0, tail = -1;

            for(int k = 0; k * v + r <= C; k++){
                long val = preDp[k * v + r] - (long)k * w;

                // 维护单调递减队列
                while(head <= tail && val >= preDp[q[tail] * v + r] - (long)q[tail] * w){
                    tail--;
                }

                tail++;
                q[tail] = k;

                // 移除滑出窗口的元素
                while(head <= tail && q[head] < k - d){
                    head++;
                }

                int bK = q[head];
                dp[k * v + r] = (preDp[bK * v + r] - (long)bK * w) + (long)k * w;
            }
        }
    }
}
image-20251206113746205