使用Markdown语法编写数学公式

在Markdown中使用LaTeX语法编写数学公式起始是一个乍一看很费劲不方便的事情，但是貌似没有别的更好更优秀的通用数学显示了，所以来学习一下这个语法

插入公式的基本语法

  • 行内公式 $ 公式内容 $，在这两个美元符号之间输入LaTex语法，即可实现在行内插入公式。

    质能公式：E = mc2
    二次方程根：$x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$

    1
    2
    质能公式：$E = mc^2$  
    二次方程根：$x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$
    1
    2
    质能公式：$E = mc^2$  
    二次方程根：$x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$

  • 公式块：$$ + 回车，会出现一对$$ $$的符号，在这一对符号之间输入LaTex语法，即可实现在行间插入公式。

    牛顿第二定律：
    F = ma
    或
    [ F = ma ]

    1
    2
    3
    4
      牛顿第二定律：  
      $$ F = ma $$  
      或  
    \[ F = ma \]
    • 貌似 \[...\] 包裹，也可以，但是typora是解析不出来的，就不用了

美元符号需在英文输入法下进行输入。中文输入法是 ￥

插入希腊字母

希腊字母的LaTex语法见下图

img
希腊字母/希伯来字母 读音（LaTeX 表示） 希腊字母/希伯来字母 读音（LaTeX 表示） 希腊字母/希伯来字母 读音（LaTeX 表示）
α κ ψ
β λ ρ
χ μ σ
δ ν τ
ε ο o θ
η ω υ
γ ϕ ξ
ι π ζ
F ε Δ
ϰ ϖ Γ
φ ϱ Λ
Ω ϕ Θ
Υ Π Ξ
Ψ Σ א
ב ד ג

α β γ δ ϵ ζ α

1
2
3
4
5
6
7
8
9
10
11
$\alpha$
$\beta$
$\gamma$
$\delta$
$\epsilon$
$\zeta$
 
 $$
 \alpha
 $$

唉 4k 吃。。。。

插入定界符号

总览图

img
符号 LaTeX代码 解释
| 竖线，可用于表示绝对值、矩阵元素分隔等
{ { 左花括号，常用于集合、分段函数定义等
⌊ 左向下取整符号，用于表示向下取整函数
/ / 除号或表示斜向的分隔
⇑ 大向上箭头
⌞ 左下直角符号
∥ 表示平行，如两直线平行
} } 右花括号
⌋ 右向下取整符号
∖ 反斜杠，在数学中有时用于集合运算表示差集等
↑ 向上箭头
⌟ 右下直角符号
‖ 双竖线，可用于表示范数等
⟨ 左尖括号，常用于表示内积等
⌈ 左向上取整符号，用于表示向上取整函数
[ [ 左方括号，常用于区间表示等
⇓ 大向下箭头
⌜ 左上直角符号
⌝ 右下直角符号
] ] ] 右方括号

举例

∖ ∥

1
2
$$\backslash$$
$$\|$$

括号之间可以更改大小以实现嵌套

img

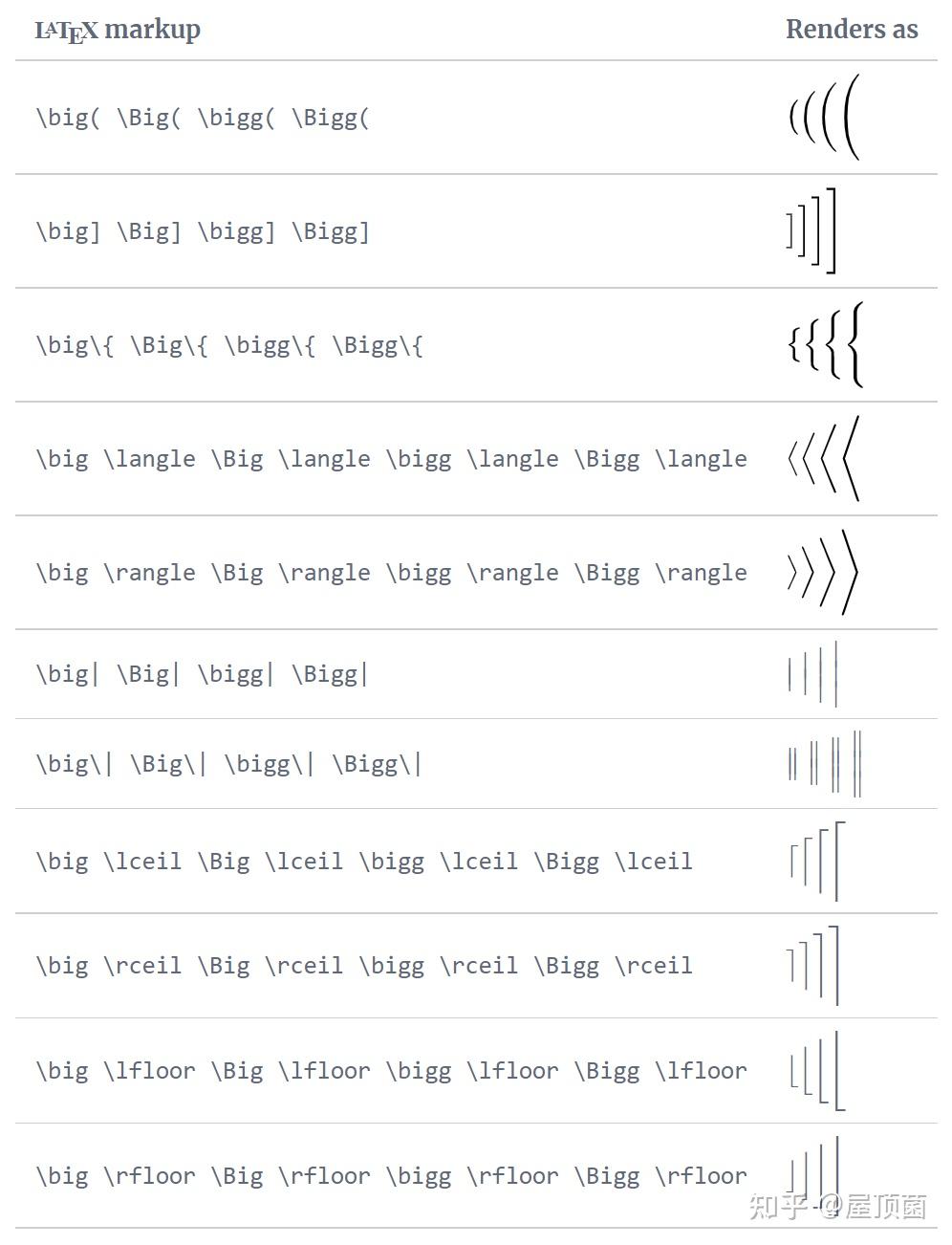
插入矩阵

矩阵中的各元素通过用$来分隔，\\来换行。 $$ \begin{matrix} 0&1&2\\ 3&4&5\\ 6&7&8\\ \end{matrix} $$

 
1
2
3
4
5
6
7
8
$$
 \begin{matrix}
 0&1&2\\
 3&4&5\\
 6&7&8\\
 \end{matrix}
$$

$$ \begin{Vmatrix} 0&1&2\\ 3&4&5\\ 6&7&8\\ \end{Vmatrix} $$

1
2
3
4
5
\begin{Vmatrix}
0&1&2\\
3&4&5\\
6&7&8\\
\end{Vmatrix}

输出分段函数

用\begin{cases}和\end{cases}来构造分段函数，中间则用\\来分段: $$ f(x) = \begin{cases} 2x,\,\,x>0\\ 3x,\,\,x\le0\\ \end{cases} $$

1
2
3
4
5
f(x) = 
\begin{cases}
2x,\,\,x>0\\
3x,\,\,x\le0\\
\end{cases}

输出方程组

使用 \begin{cases} ... \end{cases}，中间则用\\来分段: $$ f(x) = \begin{cases} 0, & x < 0 \\ 1, & x \geq 0 \end{cases} $$

1
2
3
4
f(x) = \begin{cases}
0, & x < 0 \\
1, & x \geq 0
\end{cases}

匹配内容

将上述定界符与\left和right组合使用可以使得定界符匹配其内容的高度。

比如要构建一个如下的矩阵的行列式： $$ \left| \begin{matrix} a & b & c & 1 \\ d & e & f & \epsilon\\ g & h & i & n \end{matrix} \right| $$

1
2
3
4
5
6
7
\left|
  \begin{matrix}
   a & b & c & 1 \\
   d & e & f & \epsilon\\
   g & h & i & n
  \end{matrix} 
 \right|

插入运算符号

总览图

img

×、*、÷、±、∓、≤、≥、≶

1
$\times$、$\ast$、$\div$、$\pm$、$\mp$、$\leq$、$\geq$、$\lessgtr$

这里我挑出一些常用的给大家列出来：

符号 LaTeX代码 解释
+ + 加法运算符号
− - 减法运算符号
× 乘法运算符号
÷ 除法运算符号
⋅ 点乘符号，用于乘法、函数复合等
± 正负号
∓ 与±相反的符号
∩ 集合交集运算符号
∪ 集合并集运算符号
≡ 恒等于、同余（数论）
≅ 同构（代数）、全等（几何）
≠ 不等于
≈ 约等于
∼ 相似（几何）、等价（代数）等
∈ 属于（集合论）
∉ 不属于（集合论）
⊆ 子集关系
⊇ 超集关系
⊊ 真子集关系
⊋ 真超集关系
≤ 小于等于
≥ 大于等于
< 小于
> 大于
∥ 平行（几何等）
⟂ 垂直、正交（向量等）
∨ 逻辑或、格论并运算
∧ 逻辑与、格论交运算
⊗ 张量积（线性代数等）
⊕ 直和（线性代数）、异或（逻辑）
∫ 积分符号
∑ 求和符号
∏ 求积符号
lim  极限符号
∞ 无穷大
$\sqrt{}$ 平方根符号
$\sqrt[n]{}$ n次方根符号
≈ 近似等于
≐ 近似等于、定义为
∝ 成正比
| 竖线，可表示绝对值等
⟨ 左尖括号，用于内积等
⟩ 右尖括号，用于内积等
⌊ 向下取整符号
⌋ 向下取整符号
⌈ 向上取整符号
⌉ 向上取整符号

插入数学结构

总览图

img
符号 LaTeX代码 解释
$\frac{abc}{xyz}$ 表示分数，分子为abc，分母为xyz
$\overline{abc}$ 在abc上方加一条横线，常用于表示平均值等
$\overrightarrow{abc}$ 在abc上方加向右箭头，常表示向量
f′ f’ 表示函数f的一阶导数
$\underline{abc}$ 在abc下方加一条横线
$\overleftarrow{abc}$ 在abc上方加向左箭头
$\sqrt{abc}$ 表示abc的平方根
$\widehat{abc}$ 在abc上方加帽状符号，常用于表示傅里叶变换等中的符号
$\overbrace{abc}$ 在abc上方加花括号
$\sqrt[n]{abc}$ 表示abc的n次方根
$\widetilde{abc}$ 在abc上方加波浪线，常用于表示一些变换后的符号
$\underbrace{abc}$ 在abc下方加花括号

分式结构

  • 分式：\frac{分子}{分母}

    $\frac{a}{b}$ → $\frac{a}{b}$
    $\frac{\partial f}{\partial x}$ → $\frac{\partial f}{\partial x}$

    1
    2
    \frac{a}{b} → \frac{a}{b}  
    \frac{\partial f}{\partial x} → \frac{\partial f}{\partial x}

根式结构

  • 根式：\sqrt[n]{表达式}

    $\sqrt{2}$ → $\sqrt{2}$
    $\sqrt[3]{x+y}$ → $\sqrt[3]{x+y}$

    1
    2
    \sqrt{2} → \sqrt{2}
    \sqrt[3]{x+y} → \sqrt[3]{x+y}

上下标结构

  • 上标：用 ^，如 x^2 → x2x2

  • 下标：用 _，如 x_1 → x1x1

  • 复合上下标：用 {} 包裹多字符内容与作用范围，注意其间的连接

    xn + 1 → xn + 1
    $\sum_{i=1}^n i^2$ → $\sum_{i=1}^n i^2$

    ϵ<! − −swig42 − −>

    X23γ(n϶233) $$ \lim\limits_{x\to\infty}\exp(-x) = 0 $$

    1
    2
    3
    4
    5
    6
    7
    $x^{n+1}$ → $x^{n+1}$  
      $\sum_{i=1}^n i^2$ → $\sum_{i=1}^n i^2$
      $\epsilon^{{(n+1)}^\sqrt{2}}$
      $X_{23\gamma}({n_{\backepsilon_{233}}})$
      $$
      \lim\limits_{x\to\infty}\exp(-x) = 0
      $$

其他的也是都一样用，按照图上的查就行了

插入函数名称

所有符号都可以跟数学结构混合使用，包括数学结构也可以

img
函数名 LaTeX代码 解释
arccos  反余弦函数，是余弦函数cos 的反函数
arcsin  反正弦函数，是正弦函数sin 的反函数
arctan  反正切函数，是正切函数tan 的反函数
arg  复数的辐角，在复变函数中用于表示复数的角度
cos  余弦函数，三角函数的一种
cosh  双曲余弦函数，双曲函数的一种
cot  余切函数，三角函数中tan 的倒数
coth  双曲余切函数，双曲函数的一种
csc  余割函数，是正弦函数sin 的倒数
deg  表示角度的度数
det  行列式，用于方阵，是一个数值
dim  维数，用于表示向量空间等的维度
exp  指数函数，通常以e为底，即exp (x) = ex
gcd  最大公约数，用于求两个或多个整数的最大公因数
hom  同态，在抽象代数中用于表示两个代数结构之间的同态映射
inf  下确界，集合的最大下界
ker  核，在线性代数中表示线性变换的核空间
lg  常用对数，即以10为底的对数
lim  极限，用于表示函数或数列在某点的极限值
liminf  下极限，是数列极限相关概念
limsup  上极限，是数列极限相关概念
ln  自然对数，即以e为底的对数
log  对数函数，默认底数不定，可根据上下文确定
max  最大值，用于求一组数中的最大值
min  最小值，用于求一组数中的最小值
Pr  概率，在概率论中表示事件发生的概率
sec  正割函数，是余弦函数cos 的倒数
sin  正弦函数，三角函数的一种
sinh  双曲正弦函数，双曲函数的一种
sup  上确界，集合的最小上界
tan  正切函数，三角函数的一种
tanh  双曲正切函数，双曲函数的一种

$$ \tan(at-n\pi)\\ \sin\\ \cos\\ \log\\ $$

1
2
3
4
\tan(at-n\pi)\\
\sin\\
\cos\\
\log\\

插入可变符号

总览图

img
符号 LaTeX代码 解释
∑ 求和符号，用于表示对一系列数求和
∫ 积分符号，用于表示积分运算
⨄ 不相交并集符号，用于表示集合的不相交并运算
⨁ 直和符号，常用于线性代数等领域表示向量空间的直和
⋁ 逻辑或（在格论等中表示并运算）符号
∏ 求积符号，用于表示对一系列数求乘积
∮ 闭合曲线积分符号，用于表示在闭合曲线上的积分
⋂ 交集符号，用于表示集合的交集运算
⨂ 张量积符号，用于表示张量之间的乘积运算
⋀ 逻辑与（在格论等中表示交运算）符号
∐ 余积符号，在范畴论等中有应用
∬ 二重积分符号，用于表示对二元函数的积分
⋃ 并集符号，用于表示集合的并集运算
⨀ 一种广义的乘法运算符号
⨆ 无交并集符号，强调集合元素不相交的并集

补充说明：

  1. 第一列为原图左侧符号，第三列为原图右侧符号
  2. \text{}包裹的内容为原图自定义标签，非标准LaTeX符号
  3. 标准符号已用$$...$$标记确保在Markdown中正确显示大小
  4. 原图第三行存在排版混乱，已按原始内容保留

⋂⋃⨁⨂∑∫∮∬

1
2
3
$$
\bigcap\bigcup\bigoplus\bigotimes\sum\int\oint\iint
$$

积分

积分：\int_{下限}^{上限} $$ \int_{0}^{\infty} e^{-x} dx = 1$ → $\int_{0}^{\infty} e^{-x} dx = 1 $$

1
$\int_{0}^{\infty} e^{-x} dx = 1$ → $\int_{0}^{\infty} e^{-x} dx = 1$

求和，连乘积

求和/连乘积：\sum 和 \prod $$ \sum_{i=1}^n i = \frac{n(n+1)}{2} → \sum_{i=1}^n i = \frac{n(n+1)}{2} $$

1
$\sum_{i=1}^n i = \frac{n(n+1)}{2}$ → $\sum_{i=1}^n i = \frac{n(n+1)}{2}$

$$ \prod_{\alpha = 2}^n \alpha $$

1
\prod_{\alpha = 2}^n \alpha

插入箭头符号

总表

img

这里我挑出一些常用的给大家，方便查找：

符号 LaTeX代码 解释
← 向左箭头，常用于表示映射方向、数列极限趋近方向等
⇐ 向左双箭头，在逻辑中可表示逻辑蕴含的反向
→ 向右箭头，用于表示函数映射方向、趋向等
⇒ 向右双箭头，在逻辑中表示逻辑蕴含
↔︎ 双向箭头，可表示双向映射、等价关系等
⇔ 双向双箭头，在逻辑中表示等价关系
↑ 向上箭头，可用于表示递增、上极限方向等
↓ 向下箭头，可用于表示递减、下极限方向等
↕ 上下双向箭头，可表示某种上下变化或可逆的过程
↦ 映射符号，用于表示函数中元素的对应关系
↦ 长映射符号，强调映射关系，常用于更正式的数学定义中
↗ 向右上箭头，可表示方向、趋势等
↘ 向右下箭头，可表示方向、趋势等
↙ 向左下箭头，可表示方向、趋势等
↖ 向左上箭头，可表示方向、趋势等

插入其他符号

img

♡、∞、∭、∂

1
$\heartsuit$、$\infty$、$\iiint$、$\partial$

这个我也挑出一些常用的给大家，方便查找：

符号 LaTeX代码 解释
∞ 无穷大，在极限、集合基数等概念中常用
∇ nabla算子，在向量分析中表示梯度、散度、旋度等
∂ 偏导数符号，用于多元函数求偏导
∀ 全称量词，表示“对于所有的”
∃ 存在量词，表示“存在”
∅ 空集符号，表示不含任何元素的集合
∠ 角的符号，用于表示角度
∡ 用于强调角度测量的符号
⋯ 省略号，用于表示序列等的延续
⋮ 垂直省略号，常用于矩阵、数列等表示
⋱ 斜向省略号，常见于矩阵表示中
ℑ 表示复数的虚部
ℜ 表示复数的实部
△ 三角形符号，可用于表示三角形相关概念
′ 撇号，常用于表示导数、转置等
♮ 自然符号，在音乐理论等领域有应用，在数学中有时用于特定结构

字体

字体风格

更多详见：Font sizes, families, and styles

img

数学字体

  • 罗马字体（Roman） \mathrm

    sin(x) + cos(x)

1
$\mathrm{sin}(x) + \mathrm{cos}(x)$

  • 粗体（Bold） \mathbf

    A ⋅ x = b

    1
    $\mathbf{A} \cdot \mathbf{x} = \mathbf{b}$

  • 斜体 \mathit

    在 LaTeX 中，数学公式默认使用斜体字体。但如果你想明确指定为斜体，可以使用 \mathit 命令。

    abc

    1
    $\mathit{abc}$

  • 花体

    使用 \mathcal 命令可以将公式中的部分内容设置为花体字体，常用于表示集合、范畴等。

    ℱ

    1
    $\mathcal{F}$

  • 黑板粗体（Blackboard bold）

    使用 \mathbb 命令可以将公式中的部分内容设置为黑板粗体，常用于表示数集

    ℝ, ℕ, ℤ

    1
    $\mathbb{R}, \mathbb{N}, \mathbb{Z}$

  • 哥特体

    使用 \mathfrak 命令可以将公式中的部分内容设置为哥特体字体，常用于表示李代数、理想等。

    𝔤, 𝔥

    1
    $\mathfrak{g}, \mathfrak{h}$

更多详见：Mathematical fonts

字体大小

在 LaTeX 中，可以使用不同的命令来调整字体的大小，以下是一些常用的字体大小调整命令

命令 字体大小
\tiny 极小号字体
\scriptsize scriptsize 号字体
\footnotesize footnotesize 号字体
\small 小号字体
\normalsize 正常大小字体
\large 大号字体
\Large 更大号字体
\LARGE 非常大号字体
\huge 巨大号字体
\Huge 超级巨大号字体 
1
2
3
4
5
6
7
8
9
10
$\tiny x + y$
$\scriptsize x + y$
$\footnotesize x + y$
$\small x + y$
$\normalsize x + y$
$\large x + y$
$\Large x + y$
$\LARGE x + y$
$\huge x + y$
$\Huge x + y$

$\tiny x + y$ $\scriptsize x + y$ $\small x + y$ $\normalsize x + y$ $\large x + y$ $\Large x + y$ $\LARGE x + y$ $\huge x + y$ $\Huge x + y$

对齐

多行公式对齐（align环境）

使用\begin{align}和\end{align}，&指定对齐位置： $$ \begin{align} f(x) &= (x+1)^2 \\ &= x^2 + 2x + 1 \\ \int f(x)dx &= \frac{1}{3}x^3 + x^2 + x + C \end{align} $$

1
2
3
4
5
6
7

\begin{align}
f(x) &= (x+1)^2 \\
     &= x^2 + 2x + 1 \\
\int f(x)dx &= \frac{1}{3}x^3 + x^2 + x + C
\end{align}

多公式居中（gather环境）

$$ \begin{gather} a = b + c \\ d = e^f + g \\ \lim_{x\to0}\frac{\sin x}{x} = 1 \end{gather} $$

1
2
3
4
5
6
7

\begin{gather}
a = b + c \\
d = e^f + g \\
\lim_{x\to0}\frac{\sin x}{x} = 1
\end{gather}

分段函数对齐（cases环境）

$$ f(x) = \begin{cases} x^2 & \text{if } x \geq 0 \\ -{\color{red}x^3} & \text{if } x < 0 \end{cases} $$

1
2
3
4
5
6

f(x) = \begin{cases}
x^2 & \text{if } x \geq 0 \\
-{\color{red}x^3} & \text{if } x < 0
\end{cases}

矩阵对齐（array环境）

$$ \left[ \begin{array}{cc|c} 1 & 2 & 3 \\ \hline 4 & \color{blue}5 & 6 \\ 7 & 8 & 9 \end{array} \right] $$

1
2
3
4
5
6
7
8
9
10
$$
\left[
\begin{array}{cc|c} 
1 & 2 & 3 \\ 
\hline
4 & \color{blue}5 & 6 \\
7 & 8 & 9
\end{array}
\right]
$$

拆分、对齐方程

用 & 指定对齐位置，\\ 换行： $$ \begin{align} f(x) &= (x+1)^2 + 3 \label{eq1} \\ &= x^2 + 2x + 4 \label{eq2} \\ \int f(x)dx &= \frac{1}{3}x^3 + x^2 + 4x + C \label{eq3} \end{align} $$

1
2
3
4
5
6
7
$$
\begin{align}
f(x) &= (x+1)^2 + 3 \label{eq1} \\
     &= x^2 + 2x + 4 \label{eq2} \\
\int f(x)dx &= \frac{1}{3}x^3 + x^2 + 4x + C \label{eq3}
\end{align}
$$

多列对齐 $$ \begin{align} a &= b & x &= y \\ c &= d & z &= w \end{align} $$

1
2
3
4
5
6
$$
\begin{align}
a &= b & x &= y \\
c &= d & z &= w
\end{align}
$$

居中显示方程（不以等号对齐）

gather 环境 $$ \begin{gather} a = b + c \\ d = e^f + g \notag \\ \lim_{x\to0}\frac{\sin x}{x} = 1 \end{gather} $$

1
2
3
4
5
6

\begin{gather}
a = b + c \\
d = e^f + g \notag \\  % 取消单行编号
\lim_{x\to0}\frac{\sin x}{x} = 1
\end{gather}

单行居中

$$ \boxed{E = mc^2} $$

1
$$ \boxed{E = mc^2} $$

综合对齐

$$ \begin{align} \color{red}\nabla \cdot \mathbf{E} &= \frac{\rho}{\epsilon_0} \\ \color{blue}\nabla \times \mathbf{E} &= -\frac{\partial \mathbf{B}}{\partial t} \\ \color{green}\int_{\partial \Omega} \omega &= \int_\Omega d\omega \quad \text{(Stokes定理)} \end{align} $$

1
2
3
4
5
6
7
$$
\begin{align}
\color{red}\nabla \cdot \mathbf{E} &= \frac{\rho}{\epsilon_0} \\
\color{blue}\nabla \times \mathbf{E} &= -\frac{\partial \mathbf{B}}{\partial t} \\
\color{green}\int_{\partial \Omega} \omega &= \int_\Omega d\omega \quad \text{(Stokes定理)}
\end{align}
$$

间距控制

img

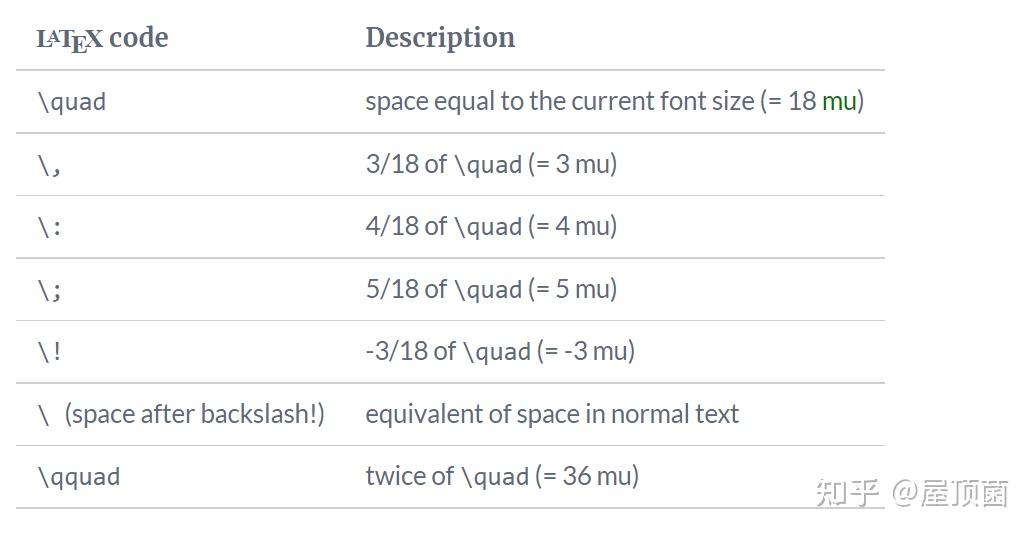
1. 水平间距

命令 间距大小 示例
\, 小空格 (3/18em) $x\,y$ → x yxy
\: 中空格 (4/18em) $x\:y$ → x yxy
\; 大空格 (5/18em) $x\;y$ → x  yxy
\quad 1em $x\quad y$ → xyxy
\qquad 2em $x\qquad y$ → xyxy
\! 负间距 (-3/18em) $x\!y$ → x ⁣yxy

2. 垂直间距

在换行时添加间距（仅在某些环境中有效）： $$ \begin{align} f(x) &= x^2 \\[5pt] f'(x) &= 2x \\[10pt] f''(x) &= 2 \end{align} $$

1
2
3
4
5
\begin{align}
f(x) &= x^2 \\[5pt]      % 增加5pt间距
f'(x) &= 2x \\[10pt]     % 增加10pt间距
f''(x) &= 2
\end{align}

3. 矩阵间距调整

$$ \begin{pmatrix} 1 & \frac{1}{2} \\[6pt] 3 & \frac{1}{4} \end{pmatrix} $$

1
2
3
4
5

\begin{pmatrix}
1 & \frac{1}{2} \\[6pt]  
3 & \frac{1}{4}
\end{pmatrix}

颜色

基础颜色语法

在LaTeX数学公式中使用\color{颜色名}命令设置颜色： x + y = z

1
2
3
$$ 
\color{red} x + \color{blue} y = \color{green} z 
$$

常用颜色名称

颜色名 示例
red \color{red} text
blue \color{blue} text
green \color{green} text
yellow \color{yellow} text
cyan \color{cyan} text
magenta \color{magenta} text
black \color{black} text
white \color{white} text
gray \color{gray} text
darkred \color{darkred} text

RGB自定义颜色

使用\color[rgb]{R,G,B}格式（值范围0-1）： $$ \color[rgb]{0.5,0.2,0.8} f(x) = \sqrt{x} $$

1
2
3
$$
\color[rgb]{0.5,0.2,0.8} f(x) = \sqrt{x}
$$

局部着色

用花括号限定作用范围： x + y<! − −swig43 − −>

1
2
3
$$
{\color{red}x} + {\color{blue}y}^{{\color{green}2}}
$$

注意事项

  • 空格处理：LaTeX 默认忽略空格，需用 \, 或 \quad 添加空格，如 x\,y → x yxy。

  • 转义字符：在公式中直接书写 #, %, _ 等符号需用 \ 转义，如 \# → ##, \% → %%。

  • 多行对齐：使用 aligned 环境实现公式对齐：

    $$ \begin{aligned} f(x) &= (x + 1)^2 \\ &= x^2 + 2x + 1 \end{aligned} $$

    1
    2
    3
    4
    \begin{aligned}
    f(x) &= (x + 1)^2 \\
         &= x^2 + 2x + 1
    \end{aligned}

之后再有用到的再补充，感觉够多了