数学物理方程波动方程的解法之达朗贝尔方法

波动方程的求解

波动方程是描述波传播现象的基本偏微分方程，在物理、工程等领域有着广泛应用，例如弦的振动、声波、电磁波的传播等。理解波动方程的解法及其物理意义是数理方程学习的核心内容之一

达朗贝尔公式

达朗贝尔公式解法也叫行波法，旨在一维波动方程求定解问题，主要用于求解无界区域内的一维波动方程定解问题。尽管其适用范围有限，但它在波动问题中具有独特的优点，是数理方程的基本解法之一。

因为行波法只能用于求解无界区域内波动方程的定解问题。虽有很大的局限性，但对于波动问题有其特殊的优点，所以该法是数理方程的基本解法之一。

弦振动方程的达朗贝尔解法

问题和方程的引入

如果我们所考察的弦线长度很长，而我们需要知道的又只是在较短时间且离开边界较远的一段范围内的振动情况，那么边界条件的影响就可以忽略，所以不妨把所考察弦线的长度视为无限。

我们首先考察无限长弦的自由振动问题，其定解问题形式如下： $$ \begin{cases} u_{tt} = a^2 u_{xx} + f(x, t) & (-\infty < x < +\infty, t > 0), \quad (1) \\ u(x, 0) = \varphi(x), \quad u_t(x, 0) = \psi(x) & (2) \end{cases} $$ 对于上述初值问题，由于微分方程及定解条件都是线性的，所以叠加原理同样成立。

即如果 u₁(x, t) 和 u₂(x, t) 分别是下述初值的问题 $$ \begin{cases} u_{tt} = a^2 u_{xx} & (-\infty < x < +\infty,\ t > 0), \\ u(x, 0) = \varphi(x),\ u_t(x, 0) = \psi(x) \end{cases} \quad \text{(3)} $$ 和 $$ \begin{cases} u_{tt} = a^2 u_{xx} + f(x, t) & (-\infty < x < +\infty,\ t > 0), \\ u(x, 0) = 0,\ u_t(x, 0) = 0 \end{cases} \quad \text{(5)} $$

的解，则 $\boxed{u = u_1(x, t) + u_2(x, t)}$ 是原问题 (1)(2) 的解。

$$ \begin{cases} u_{tt} = a^2 u_{xx} & (-\infty < x < +\infty,\ t > 0), \text{(3)}\\ u(x, 0) = \varphi(x),\ u_t(x, 0) = \psi(x) \quad \text{(4)} \end{cases} \quad $$

首先我们考察问题(3)(4)，通过自变量变换求解。

对于齐次的初始值问题（方程 u_tt − a²u_xx = 0 (3) 配合上述初始条件 (4)），开始进行详细的求解

坐标变换与方程化简

为了求解问题 (3)(4)，我们引入特征线坐标变换：

$$ \begin{cases} \xi = x - at \\ \eta = x + at \end{cases} \quad \text{(7)} $$

其逆变换为：

$$ \begin{cases} x = \frac{\xi + \eta}{2} \\ t = \frac{\eta - \xi}{2a} \end{cases} \quad \text{(8)} $$

令新的未知函数为 u(ξ, η)。利用复合函数微分法则，我们可以推导出 u_tt 和 u_xx 在新坐标系下的表达式：

首先计算一阶偏导： $$ u_x = \frac{\partial u}{\partial \xi} \frac{\partial \xi}{\partial x} + \frac{\partial u}{\partial \eta} \frac{\partial \eta}{\partial x} = u_\xi \cdot 1 + u_\eta \cdot 1 = u_\xi + u_\eta $$

$$ u_t = \frac{\partial u}{\partial \xi} \frac{\partial \xi}{\partial t} + \frac{\partial u}{\partial \eta} \frac{\partial \eta}{\partial t} = u_\xi \cdot (-a) + u_\eta \cdot a = a(u_\eta - u_\xi) $$

接着计算二阶偏导： $$ u_{xx} = \frac{\partial}{\partial x}(u_\xi + u_\eta) = \frac{\partial}{\partial \xi}(u_\xi + u_\eta) \frac{\partial \xi}{\partial x} + \frac{\partial}{\partial \eta}(u_\xi + u_\eta) \frac{\partial \eta}{\partial x} = (u_{\xi\xi} + u_{\eta\xi}) \cdot 1 + (u_{\xi\eta} + u_{\eta\eta}) \cdot 1 = u_{\xi\xi} + 2u_{\xi\eta} + u_{\eta\eta} \quad \text{(9)} $$

$$ u_{tt} = \frac{\partial}{\partial t}(a(u_\eta - u_\xi)) = \frac{\partial}{\partial \xi}(a(u_\eta - u_\xi)) \frac{\partial \xi}{\partial t} + \frac{\partial}{\partial \eta}(a(u_\eta - u_\xi)) \frac{\partial \eta}{\partial t} = a(u_{\eta\xi} - u_{\xi\xi})(-a) + a(u_{\eta\eta} - u_{\xi\eta})(a) = a^2(u_{\xi\xi} - 2u_{\xi\eta} + u_{\eta\eta}) \quad \text{(10)} $$

将 (9) 和 (10) 代入波动方程 (3) u_tt − a²u_xx = 0： a²(u_ξξ − 2u_ξη + u_ηη) − a²(u_ξξ + 2u_ξη + u_ηη) = 0

化简得到： −4a²u_ξη = 0 ⇒ u_ξη = 0 (11)

通解的求解

之后进行通解的求解

方程 (11) 可以通过积分直接求解。先关于 ξ 积分一次，再关于 η 积分一次，得到通解为：

u(ξ, η) = F(η) + G(ξ) (12) 其中 F 和 G 是具有二阶连续导数的任意函数。

将变量变换 (7) 代回 (12)，即可得到方程 (3) 的通解： u(x, t) = F(x + at) + G(x − at) (13)

利用初始条件确定任意函数

我们利用初始条件 (4) 来确定通解 (13) 中的 F 和 G。

将 t = 0 代入 (13) 和其对 t 的导数： u(x, 0) = F(x) + G(x) = ϕ(x) (14)

u_t(x, t) = aF^′(x + at) − aG^′(x − at)

$$ u_t(x,0) = aF'(x) - aG'(x) = \psi(x) \Rightarrow F'(x) - G'(x) = \frac{1}{a}\psi(x) \quad \text{(15)} $$

对 (15) 两边积分，得到： $$ F(x) - G(x) = \frac{1}{a}\int_{x_0}^x \psi(\alpha) d\alpha + C \quad \text{(16)} $$

现在我们有关于 F(x) 和 G(x) 的线性方程组： $$ \begin{cases} F(x) + G(x) = \phi(x) \\ F(x) - G(x) = \frac{1}{a}\int_{x_0}^x \psi(\alpha) d\alpha + C \end{cases} $$

联立解得： $$ F(x) = \frac{1}{2}\phi(x) + \frac{1}{2a}\int_{x_0}^x \psi(\alpha) d\alpha + \frac{C}{2} $$

$$ G(x) = \frac{1}{2}\phi(x) - \frac{1}{2a}\int_{x_0}^x \psi(\alpha) d\alpha - \frac{C}{2} $$

将 x + at 代替 x 到 F(x) 中，将 x − at 代替 x 到 G(x) 中，再代入通解 (13)： $$ u(x,t) = \left( \frac{1}{2}\phi(x+at) + \frac{1}{2a}\int_{x_0}^{x+at} \psi(\alpha) d\alpha + \frac{C}{2} \right) + \left( \frac{1}{2}\phi(x-at) - \frac{1}{2a}\int_{x_0}^{x-at} \psi(\alpha) d\alpha - \frac{C}{2} \right) $$

$$ u(x,t) = \frac{1}{2}[\phi(x+at) + \phi(x-at)] + \frac{1}{2a}\left( \int_{x_0}^{x+at} \psi(\alpha) d\alpha - \int_{x_0}^{x-at} \psi(\alpha) d\alpha \right) $$

$$ u(x,t) = \frac{1}{2}[\phi(x+at) + \phi(x-at)] + \frac{1}{2a}\int_{x-at}^{x+at} \psi(\alpha) d\alpha \quad \text{(18)} $$

这就是无限长弦自由振动的达朗贝尔公式，或称达朗贝尔解。

这种求解方法就是达朗贝尔解法。

$$ \begin{cases} u_{tt} = a^2 u_{xx} & (-\infty < x < +\infty,\ t > 0), \\ u(x, 0) = \varphi(x),\ u_t(x, 0) = \psi(x) \end{cases} \quad \text{(3)} $$

u(x, t) = f(x − at) + g(x + at) (13)

达朗贝尔解的物理意义

从通解 (13) 式 u(x, t) = F(x + at) + G(x − at) 可见，自由弦振动方程的解可以表示成两个函数之和，可以表示成形如 $f(x-at) $ 和 g(x + at) 的两个函数之和，通过它们可以清楚地看出波动传播的性质。

函数 G(x − at) 描述的振动波形以常速度 a 向右传播，称为右传播波
函数 F(x + at) 描述的振动波形以常速度 a 向左传播，称为左传播波

波动方程 (3) 中出现的常数 a 正好是波的传播速度。这表明弦上的任意扰动总是以行波形式分别向两个方向传播出去。振动的波动性和传播的有限性是振动的两个基本特征。

考察 u₁(x, t) = f(x − at)

证明其为波动方程的解：

这个函数 u₁(x, t) = f(x − at) 显然是方程 (3) u_tt = a²u_xx 的解。我们可以通过求偏导来验证这一点：

对 t 求一阶偏导：$\frac{\partial u_1}{\partial t} = f'(x-at) \cdot (-a)$
对 t 求二阶偏导：$\frac{\partial^2 u_1}{\partial t^2} = f''(x-at) \cdot (-a)^2 = a^2 f''(x-at)$
对 x 求一阶偏导：$\frac{\partial u_1}{\partial x} = f'(x-at) \cdot (1)$
对 x 求二阶偏导：$\frac{\partial^2 u_1}{\partial x^2} = f''(x-at) \cdot (1)^2 = f''(x-at)$

将这些代入方程 (3) u_tt = a²u_xx，我们得到 a²f^″(x − at) = a²f^″(x − at)，等式成立。

物理意义：

通过给 t 赋予不同的值，我们可以看出弦在各个时刻相应的振动状态：

在 t = 0 时，我们有 u₁(x, 0) = f(x)。这对应于初始时刻的振动状态（相当于弦在初始时刻各点的位移状态），如图 3.1 实线所示。
经过时间 t₀ 后，在 (x, t₀) 处，函数变为 u₁(x, t₀) = f(x − at₀)。在 u − x 平面上，它相当于原来的图形 f(x) 向右平移了一段距离 at₀。这意味着波形在空间中整体向右移动。
随着时间的推移，这个波形图将不断地向右移动。这说明当方程 (3) 的解表示成 f(x − at) 的形式时，振动的波形是以常速度 a 向右传播。因此，由函数 f(x − at) 所描述的振动规律，称为右传播波。

考察 u₂(x, t) = g(x + at)

证明其为波动方程的解：

与 f(x − at) 类似，u₂(x, t) = g(x + at) 也是方程 (3) u_tt = a²u_xx 的解：

对 t 求二阶偏导：$\frac{\partial^2 u_2}{\partial t^2} = g''(x+at) \cdot (a)^2 = a^2 g''(x+at)$
对 x 求二阶偏导：$\frac{\partial^2 u_2}{\partial x^2} = g''(x+at) \cdot (1)^2 = g''(x+at)$

同样满足 u_tt = a²u_xx。

物理意义：

同样，形如 g(x + at) 的函数描述的振动波形是以常速度 a 向左传播。当 t 增加时，为了保持 x + at 不变（即保持波形上的某个特定点），x 必须减小，这表示波形向左移动。它所描述的振动规律，称为左传播波。

总结达朗贝尔解的物理意义

从达朗贝尔公式 u(x, t) = f(x − at) + g(x + at) 可见，弦上的任意扰动总是以行波形式分别向两个方向传播出去。
其传播速度正好是方程 (3) 中出现的常数 a。
振动的波动性和传播的有限性是振动的两个基本特征。
这样，弦振动方程的解为左右传播波的叠加。这体现了波动方程的线性性质，使得其解可以通过叠加不同形式的波来构建。
因此，波动方程的重要特征是传播速度的有限性。

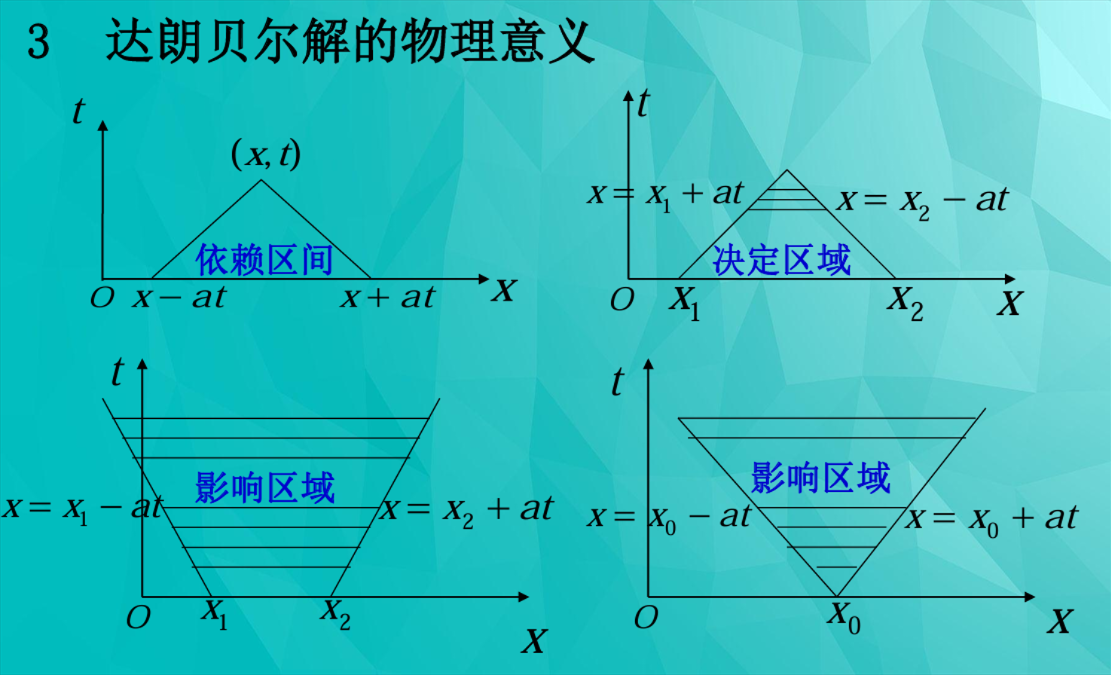
依赖区间、决定区域和影响区域

从达朗贝尔通解公式 u(x, t) = f(x − at) + g(x + at) (公式(13)) 或更具体的达朗贝尔公式： $$ u(x,t) = \frac{1}{2}[\varphi(x-at) + \varphi(x+at)] + \frac{1}{2a}\int_{x-at}^{x+at} \psi(\alpha)d\alpha \quad (18) $$ 我们可以深入理解波动传播的性质。

依赖区间 (Dependence Domain)

问题：初值问题 (3)(4) 的解 u(x, t) 在一点 (x, t) 的数值与初值条件在 x 轴上哪些点的值有关？

结论：从达朗贝尔公式 (18) 可以看到，解在点 (x, t) 的数值仅依赖于 x 轴的区间 [x − at, x + at] 上的初值条件，而与其他点上的初值条件无关。这个区间 [x − at, x + at] 称为点 (x, t) 的依赖区间。 $$ \begin{cases} u_{tt} = a^2 u_{xx} & (-\infty < x < +\infty,\ t > 0), \\ u(x, 0) = \varphi(x),\ u_t(x, 0) = \psi(x) \end{cases} \quad \text{(3)} $$

$$ u(x, t) = \frac{\varphi(x-at) + \varphi(x+at)}{2} + \frac{1}{2a}\int_{x-at}^{x+at} \psi(\alpha) d\alpha \quad \text{(18)} $$

详细解释：

达朗贝尔公式明确指出，在某个特定的时刻 t 和空间位置 x 处的弦位移 u(x, t) 的值，完全取决于初始位移函数 φ(x) 在 x − at 和 x + at 这两点的值，以及初始速度函数 ψ(x) 在 x − at 到 x + at 的整个区间上的积分值。
这意味着，为了确定 u(x, t) 的值，我们只需要知道 t = 0 时刻 x 轴上落在 [x − at, x + at] 范围内的那些点的初始位移和初始速度。
这个区间就是决定 u(x, t) 值的“过去”的范围，即该点当前状态所“依赖”的初始条件区域。

几何解释（结合图3.2）：

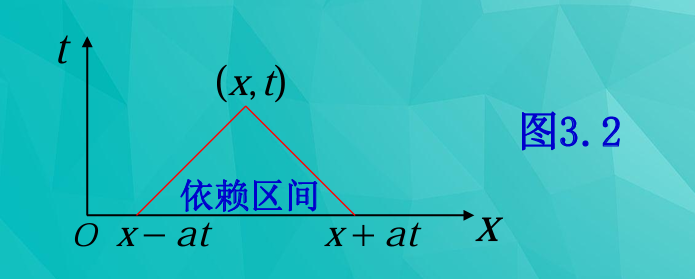
该区间 [x − at, x + at] 是通过点 (x, t) 分别作斜率为 $\frac{1}{a}$ 和 $-\frac{1}{a}$ 的直线（这些直线称为特征线）与 x 轴所交截得的区间。
在 x − t 平面上，从待求点 P(x, t) 向时间轴（t 轴）的反方向（即 t = 0 的 x 轴）引出两条直线：
- 一条直线连接 P(x, t) 和 x 轴上的点 (x − at, 0)，斜率为 $\frac{1}{a}$。
- 另一条直线连接 P(x, t) 和 x 轴上的点 (x + at, 0)，斜率为 $-\frac{1}{a}$。
这两条特征线在 x 轴上截出的区间 [x − at, x + at] 就是点 (x, t) 的依赖区间。
这形象地展示了波动传播的有限速度性质：在 t 时刻 x 处的波形，其信息来源只能是初始时刻距离其 at 范围内的点。超过这个范围的初始扰动，还未到达或已通过点 x。

决定区域 (Domain of Determination)

问题：考虑初始轴 t = 0 上的一个区间 [x₁, x₂]，其决定区域是什么？

结论：在 x − t 平面上，过点 (x₁, 0) 作斜率为 $\frac{1}{a}$ 的直线 x = x₁ + at，过点 (x₂, 0) 作斜率为 $-\frac{1}{a}$ 的直线 x = x₂ − at，这两条直线在 t > 0 的区域内相交，与 t = 0 时的区间 [x₁, x₂] 一起构成一个三角形区域。此三角形区域称为区间 [x₁, x₂] 的决定区域。 $$ \begin{cases} u_{tt} = a^2 u_{xx} & (-\infty < x < +\infty,\ t > 0), \\ u(x, 0) = \varphi(x),\ u_t(x, 0) = \psi(x) \end{cases} \quad \text{(3)} $$

$$ u(x, t) = \frac{\varphi(x-at) + \varphi(x+at)}{2} + \frac{1}{2a}\int_{x-at}^{x+at} \psi(\alpha) d\alpha \quad \text{(18)} $$

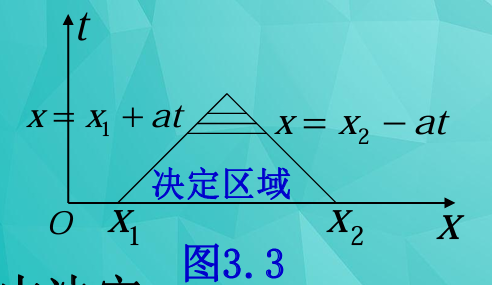
详细解释：

决定区域是“未来”的范围。如果仅仅在初始时刻 t = 0 知道 x 轴上 [x₁, x₂] 区间内的初始位移和初始速度，那么在这个三角形区域内的所有点 (x, t) 的解 u(x, t) 都可以被完全确定。
这是因为，对于这个三角形区域内的任意一点 (x, t)，其依赖区间 [x − at, x + at] 都会完全包含在 [x₁, x₂] 内部。
这进一步强调了波动传播的有限速度特性：在有限时间内，只有有限区域内的初始信息能够决定有限区域内的解。

影响区域 (Region of Influence)

问题：如果在初始时刻 t = 0 扰动仅在一有限区间 [x₁, x₂] 上存在，则经过时间 t 后，它所影响到的范围是什么呢？

我们知道，波动是以一定的速度 a 向两个方向传播

$$ \begin{cases} u_{tt} = a^2 u_{xx} & (-\infty < x < +\infty,\ t > 0), \\ u(x, 0) = \varphi(x),\ u_t(x, 0) = \psi(x) \end{cases} \quad \text{(3)} $$

$$ u(x, t) = \frac{\varphi(x-at) + \varphi(x+at)}{2} + \frac{1}{2a}\int_{x-at}^{x+at} \psi(\alpha) d\alpha \quad \text{(18)} $$

结论：波动是以一定的速度 a 向两个方向传播。因此，经过时间 t 后，它所传到的范围（受初始扰动影响到的范围）由不等式 x₁ − at ≤ x ≤ x₂ + at 决定，而在此范围之外不受影响。

详细解释：

影响区域是“未来”的扩展范围。与决定区域不同，影响区域关注的是一个初始扰动（例如，一个在 [x₁, x₂] 区间内非零的初始位移或速度）在未来时刻会影响到哪些空间点。
由于波以速度 a 向左右两边传播，初始在 x₁ 处的扰动会向左传播，在 t 时刻到达 x₁ − at；初始在 x₂ 处的扰动会向右传播，在 t 时刻到达 x₂ + at。
因此，在时刻 t，原始区间 [x₁, x₂] 内的所有扰动，其影响范围将扩散到更大的区间 [x₁ − at, x₂ + at]。

几何解释（结合图3.4）：

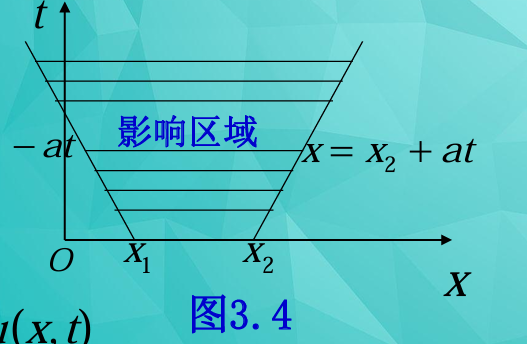
在 x − t 平面上，不等式 x₁ − at ≤ x ≤ x₂ + at 所表示的区域称为区间 [x₁, x₂] 的影响区域。
从 x 轴上的点 (x₁, 0) 向上画一条斜率为 $-\frac{1}{a}$ 的直线（方程为 x = x₁ − at）。
从 x 轴上的点 (x₂, 0) 向上画一条斜率为 $\frac{1}{a}$ 的直线（方程为 x = x₂ + at）。
这两条直线向上展开，与 t 轴围成的区域就是影响区域。
在这个影响区域中，初值问题的解 u(x, t) 的数值是受到区间 [x₁, x₂] 上初值条件的影响的；在此区域外，初值问题的解 u(x, t) 的数值则不受区间 [x₁, x₂] 上初值条件的影响。
这意味着，一旦初始扰动在某个有限区间之外是零，那么这个零值区域将随着时间以速度 a 向外扩展，并保持为零，因为波速是有限的。

特殊情况：一点 x₀ 的影响区域（结合图3.5）

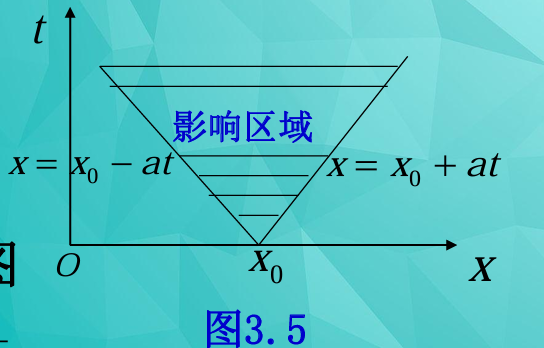
将初始扰动区间 [x₁, x₂] 收缩为 x 轴上的一个点 x₀，则可得到点 x₀ 的影响区域。它为过此点 (x₀, 0) 的两条斜率各为 $\pm \frac{1}{a}$ 的直线 x = x₀ ± at 所夹成的角形区域。
从 x 轴上的点 (x₀, 0) 向上引出两条特征线：一条斜率为 $-\frac{1}{a}$ (x = x₀ − at)，另一条斜率为 $\frac{1}{a}$ (x = x₀ + at)。
这两条直线在 t > 0 的区域内形成一个V形区域，被称为影响锥（或特征锥）。
它表示在初始时刻 t = 0 仅在 x₀ 处发生的一个瞬时扰动，在未来能够传播并影响到的所有时空点。在影响锥之外的区域，扰动是无法到达的。
这再次强调了波动方程所描述的物理现象中，扰动的传播速度是有限的，而不是无限快。

齐次化原理

$$ \begin{cases} u_{tt} = a^2 u_{xx} + f(x, t) & (-\infty < x < +\infty,\ t > 0), \\ u(x, 0) = \varphi(x),\ u_t(x, 0) = \psi(x) \end{cases} \quad \text{(1)} $$

$$ \begin{cases} u_{tt} = a^2 u_{xx} & (-\infty < x < +\infty,\ t > 0), \\ u(x, 0) = \varphi(x),\ u_t(x, 0) = \psi(x) \end{cases} \quad \text{(3)} $$