洛谷P1631序列合并Java题解

题目分析

给定两个长度为 N 的有序数组 $A = \\{a_1, a_2, \ldots, a_N\\}$ 和 $B = \\{b_1, b_2, \ldots, b_N\\}$，求所有 a_i + b_j 组合中的前 N 个最小和。

思路

开个 N^2 大小的数组，直接计算所有 N² 个和并排序的时间复杂度为 O(N²log N)，这在 N ≤ 10⁵ 时显然不可行。

有序数组存在特性：数组 A 和 B 已分别按升序排列，因此对于固定的 a_i，a_i + b_j 的值随 j 增大而单调递增。

考虑使用堆，观察题中的两个数组： [ a 1 , a 2 , … , a N ] ， [ b 1 , b 2 , … , b N ]，对这两个数组分别从小到大排序，变成两个有序队列。这样，从A和B中各任取一个数相加得到N^2个和，可以把这些和看成形成了n个有序表/队列：

考虑多路归并：
将每个 a_i 与 B 数组相加得到的序列视为一个有序队列，则总共有 N 个有序队列： $$ \begin{aligned} Q_1 &: a_1 + b_1,\ a_1 + b_2,\ \ldots,\ a_1 + b_N \\ Q_2 &: a_2 + b_1,\ a_2 + b_2,\ \ldots,\ a_2 + b_N \\ &\vdots \\ Q_N &: a_N + b_1,\ a_N + b_2,\ \ldots,\ a_N + b_N \\ \end{aligned} $$ 我们的目标是合并这些队列，找到前 N 小的元素。

由所有的 a i + b j 便可以组成以下 N 个偏序集:

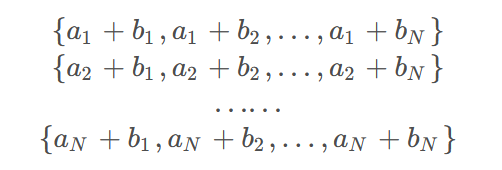
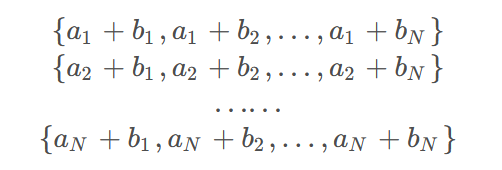
显然，在这 N 个偏序集中，都能够保证是有序的（单调递增）

因此，对每个单独的偏序集而言，其始终满足：ai + bj <= ai + b(j+1)

同时，可断言 a 1 + b 1 为所有 a i + b j 组合中的最小值； a N + b N 为所有 a i + b j 组合中的最大值；

所以，我们就能在 O(1) 的时间复杂度内，从构建好的偏序集中取出当前最小值

使用最小堆维护当前所有队列的队首元素。每次取出堆顶元素（当前最小值），并将该元素所在队列的下一个元素加入堆中。

建堆和取值策略如下：

把每个偏序集中的最小元素加入到小根堆 heap 中，即 heap = {a1+b1,a2+b1,…,aN+b1} ；
从小根堆 h e a p heap heap 中取出根元素（即当前堆里的最小值），假设取出的元素为 a i + b j，记弹出数 +1；
从取出元素所在的偏序集中，取出仅比此小的元素，ai + b (j+1)，将其插入到小根堆 heap 中
若弹出数不为 N，则继续执行 2；否则结束取值

初始化堆
将每个队列的第一个元素（即 a_i + b₁）加入堆，记录对应的 i 和当前 b 的索引 j = 1。
迭代取最小值
重复 N 次：
- 取出堆顶元素 a_i + b_j，加入结果集。
- 若 j + 1 ≤ N，将 a_i + b_j + 1 加入堆中，并更新索引为 j + 1。
去重与边界处理
使用三元组 (sum, i, j) 存储堆元素，确保同一队列中不同位置的元素能被正确追踪。

复杂度分析 - 时间复杂度：O(Nlog N)，每次堆操作的时间为 O(log N)，共进行 O(N) 次。 - 空间复杂度：O(N)，堆中最多存储 N 个元素。

import java.util.Arrays;
import java.util.PriorityQueue;
import java.util.Scanner;


public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int[] a = new int[n];
        int[] b = new int[n];

        // 读取输入数据
        for (int i = 0; i < n; i++) {
            a[i] = sc.nextInt();
        }
        for (int i = 0; i < n; i++) {
            b[i] = sc.nextInt();
        }
        sc.close();

        // 对数组排序
        Arrays.sort(a);
        Arrays.sort(b);

        // 使用优先队列（小根堆）
        PriorityQueue<int[]> pq = new PriorityQueue<>((x, y) -> x[0] - y[0]);
        // 初始化堆：将每个a[i]与b[0]的和加入堆
        for (int i = 0; i < n; i++) {
            pq.offer(new int[]{a[i] + b[0], i, 0});
        }

        // 查找前 n 小的值
        StringBuilder sb = new StringBuilder();
        while(n-- > 0){
            int[] curr = pq.poll();
            int sum = curr[0];
            int aIdx = curr[1];
            int bIdx = curr[2];

            sb.append(sum).append(" ");

            // 如果当前b索引+1有效，则将下一个和加入堆
            if (bIdx + 1 < b.length) {
                pq.offer(new int[]{a[aIdx] + b[bIdx + 1], aIdx, bIdx + 1});
            }
        }

        System.out.println(sb.toString().trim());
    }
}