参数估计之点估计
什么是参数估计
首先,什么是参数估计呢?
之前我们其实已经了解到很多种分布类型了,比如正态分布、均匀分布、泊松分布等。拿正态分布举例,决定正态分布的有两个参数:均值和方差。
因此,参数就是决定分布的关键性数据。知道了参数,也就是知道了分布的详细内容。
总体的分布类别如果我们知道了,是不是只要知道分布的参数,就能知道总体的分布详情?
所以说,用样本的数据来构造函数(即统计量),来估计总体参数,这就是参数估计。
估计量
定义
估计量是样本的统计量,用于估计总体未知参数。它是一个随机变量,因为其值依赖于随机样本。
若总体参数为 θ,表示总体X的待估计参数,其中 X1, X2, …, Xn 是来自总体的样本,则其中的一个估计量记作 θ̂ = θ̂(X1, X2, …, Xn)来估计θ,则称 θ̂ 为 θ 的估计量
理解
用于估计总体参数的 随机变量 ,是基于样本构造的、对总体参数进行估计的 “规则 / 公式” 。
它本身是一种统计量(由样本数据计算得到),因样本具有随机性,所以估计量是随机变量,会随样本不同而变化。
比如:用 “样本均值 $\bar{X} = \frac{1}{n}\sum_{i = 1}^{n}X_i$” 估计 “总体均值 μ” ,这里的 X̄ 就是总体均值 μ 的一个估计量;同理,样本方差、样本比例等也可作为对应总体参数的估计量。
估计值
定义
而继续上述估计量的说法
若总体参数为 θ,表示总体X的待估计参数,其中 X1, X2, …, Xn 是来自总体的样本,则其中的一个估计量记作 θ̂ = θ̂(X1, X2, …, Xn)来估计 θ,则称 θ̂ 为 θ 的估计量,对应于样本(X1, X2, …, Xn)的一次观测值,估计量 θ̂ 的值 θ̂(X1, X2, …, Xn) 称为 θ 的估计值,并且仍然简记为 θ̂
简单说法:对于样本观测值 x1, x2, …, xn,估计值为 θ̂ = T(x1, x2, …, xn)。
理解
估计量是函数形式(如样本均值 $\bar{X} = \frac{1}{n}\sum_{i=1}^n X_i$),而估计值是函数代入样本后的具体数值(如 x̄ = 5.2)。
所以估计值是基于某一次抽样的样本,把数据代入估计量的公式,算出的具体值。由于样本确定,估计值是固定数。
比如:抽取一组样本,计算得样本均值 x̄ = 80(这里用小写 x̄ 表示具体数值 ),那么 80 就是总体均值 μ 的估计值;若换一组样本,计算出 x̄ = 82,则此时估计值就是 82 。
何为点估计
点估计就是用一个数值对总体参数给出估计;
利用样本数据计算一个数值,来直接估计总体未知参数的具体值。
用样本的 “某个特征值” 作为总体对应参数的 “最佳猜测”,结果是一个确定的数值(点),而非区间。
此时,总体与样本的关系如下
- 总体参数(如 μ, σ2, p)通常未知,需通过抽样获取样本(如 X1, X2, …, Xn)。
- 点估计的目标:用样本构造一个统计量(如 X̄, S2, P̂),将其计算值作为总体参数的近似。
点估计的方法基本如下
- 根据问题选矩估计、极大似然估计等构造估计量;
- 用样本数据计算估计值
- 用无偏性、有效性等标准评估估计的可靠性。
矩估计法
什么是矩估计呢
矩估计比较好理解,就是用样本矩直接匹配总体矩,从而估计未知参数。
- 样本矩:从实际数据计算出的统计量(如样本均值、方差)。
- 总体矩:理论分布的数字特征(如期望、方差)。
- 尽量选取低阶矩 - 总体矩必须含有未知参数。
啥意思呢?就是我们将样本的矩计算出来,直接作为总体的矩即可。
例如:
- 总体均值 μ 的矩估计量是样本均值 X̄;总体方差 σ2 的矩估计量是 $\frac{1}{n}\sum(X_i - \bar{X})^2$(注意:与无偏估计的样本方差 $S^2 = \frac{1}{n-1}\sum(X_i - \bar{X})^2$ 不同)。
矩法估计的重点就在于“矩”字,我们知道矩是概率分布的一种数字特征,可以分为原点矩和中心矩两种。对于随机变量X而言,其 k 阶原点矩和 k 阶中心矩为
离散的 k 阶原点矩: E[Xk] = ∑ixik ⋅ P(X = xi) 离散的 k 阶中心矩: $$ \mu_k = \sum_{i=1}^{n} (x_i - EX)^k p_i $$ 连续的 k 阶原点矩 E[Xk] = ∫−∞∞xkf(x) dx 连续的 k 阶中心距 μk = ∫−∞+∞(x − EX)kf(x) dx 特别地,一阶原点矩就是随机变量的期望,二阶中心矩就是随机变量的方差,由于E(X − E(X)) = 0,所以我们不定义一阶中心矩。
具体求法
设总体 X 的分布函数为 F(x : θ1, θ2, …, θn),其中θ1, θ2, …, θn,是 k 个待估参数,(X1, X2, ⋯, Xn)是取自X的样本。假设总体X的k阶原点矩E(Xk)存在,则总体X的j阶原点矩 aj(θ1, θ2, ⋯, θk) = E(Xj), 1 ≤ j ≤ k 样本(X1, X2, ⋯, Xn)的 $j $ 阶原点矩为 $$ A_j = \frac{1}{n} \sum_{i = 1}^n X_i^j,\quad 1 \leq j \leq k $$ 令样本矩等于对应的总体矩,可得 k 个方程 aj(θ1, θ2, ⋯, θk) = Aj, 1 ≤ j ≤ k (7.1) 求解上述方程组,得到一组解θ̂1, θ̂2, ⋯, θ̂k,以此作为待估参数θ1, θ2, ⋯, θk的矩估计量。
完全可以拆分成如下形式,好理解一些
- 计算样本矩:根据样本数据计算前 k 阶矩(通常只需低阶矩)。
- 例如:样本均值 $\bar{X} = \frac{1}{n}\sum_{i=1}^n X_i$(一阶原点矩),样本方差 $S^2 = \frac{1}{n}\sum_{i=1}^n (X_i - \bar{X})^2$(二阶中心矩)。
- 设定总体矩方程:将总体矩表示为待估参数 θ 的函数。
- 例如:若总体服从 N(μ, σ2),则一阶总体矩 E(X) = μ,二阶中心矩 $ D(X) = ^2$。
- 联立方程求解:令样本矩 = 总体矩,解出参数 θ。
- 例如:
- μ̂ = X̄(用样本均值估计总体均值)
- $\hat{\sigma}^2 = \frac{1}{n}\sum_{i=1}^n (X_i - \bar{X})^2$(用样本二阶中心矩估计总体方差)
- μ̂ = X̄(用样本均值估计总体均值)
- 例如:
示例
泊松分布的矩估计
设 X ∼ Poisson(λ),参数 λ 未知, λ > 0,X1, X2, …, Xn为取自X的样本,求待估参数λ的矩估计:
因为只有一个待估计参数,所以只要列出总体一阶原点矩等于样本一阶原点矩的方程就行,
- 总体一阶矩:$E(X) =
\int_{-\infty}^{\infty} x f(x; \lambda) \, dx =
\frac{1}{\lambda}$。
- 样本一阶矩:$\bar{X} = \frac{1}{n}\sum
X_i$。
- 矩估计:$\frac{1}{\lambda} = \frac{1}{n} \sum_{i=1}^{n} X_i = \overline{X}$(用样本均值估计 λ)。
解得 λ 的矩估计为$ = $
试求总体均值和方差的矩估计
设总体均值为μ,方差为σ2,(X1, X2, ⋯, Xn)为取自总体X的样本。因为待估参数为μ, σ2两个,故由矩估计法得方程组 $$ \begin{cases} a_1 = A_1, \\ a_2 = A_2, \end{cases} $$ 即 $$ \begin{cases} \mu = \frac{1}{n} \sum_{i = 1}^{n} X_i = \overline{X}, \\ \mu^2 + \sigma^2 = \frac{1}{n} \sum_{i = 1}^{n} X_i^2, \end{cases} $$ 解得 $$ \begin{cases} \hat{\mu} = \overline{X}, \\ \hat{\sigma}^2 = \frac{1}{n} \sum_{i = 1}^{n} X_i^2 - \overline{X}^2 = \frac{1}{n} \sum_{i = 1}^{n} (X_i - \overline{X})^2 \stackrel{记为}{=} \widetilde{S}^2 \end{cases} $$ 由于总体的k阶中心矩 μk = E(X − EX)k 总可以通过展开的方法化为阶数不超过 k 的总体原点矩的函数,而样本的 k 阶中心矩 $B_k = \frac{1}{n} \sum_{i = 1}^{n} (X_i - \overline{X})^k$ 同样也可展开为阶数不超过 k 的样本原点矩的函数
上述推导得出两个核心结论: 1. 总体均值 μ 的矩估计 $$ \hat{\mu} = \overline{X} = \frac{1}{n}\sum_{i=1}^n X_i $$ 直接用样本均值估计总体均值
总体方差 σ2 的矩估计 $$ \hat{\sigma}^2 = \frac{1}{n}\sum_{i=1}^n (X_i - \overline{X})^2 \triangleq \widetilde{S}^2 $$ 用样本二阶中心矩估计总体方差,注意这是有偏估计,(真实方差需用无偏估计 $S^2 = \frac{1}{n-1}\sum (X_i - \overline{X})^2$)。
但是当样本量 n → ∞ 时,S̃2 会趋近真实方差。
因此上述例子的结论可作为矩估计法推广到一般情形,即可以用样本的 k 阶中心矩作为总体的 k 阶中心矩的矩估计量。此结论很有用,在实际中很方便。
均匀分布的矩估计
设总体 X 服从 [a, b] 上的均匀分布, a, b 为待估参数,(X1, X2, ⋯, Xn) 为取自 X 的样本,求 a, b 的矩估计量 。
利用矩估计法原理:需列出总体一、二阶中心矩等于样本一、二阶中心矩的方程。
已知均匀分布 $XU[a,b] $ 的期望 $EX = $,方差 $DX=\frac{1}{12}(b - a)^2$ (方差是二阶中心矩 )。
样本一阶中心矩对应样本均值 $=_{i = 1}^{n}X_i $
样本二阶中心矩为 $^2=_{i = 1}^{n}(X_i - )^2 $。
联立矩方程: 令总体一阶原点矩(期望)等于样本一阶原点矩(样本均值),总体二阶中心矩(方差)等于样本二阶中心矩,得到方程组: $$ \begin{cases} \frac{1}{2}(a + b)=\overline{X} \\ \frac{1}{12}(b - a)^2=\frac{1}{n}\sum_{i = 1}^{n}(X_i - \overline{X})^2=\widetilde{S}^2 \end{cases} $$
通过解上述方程组,得到待估参数 $ a,b $ 的矩估计量 $$ \hat{a}=\overline{X}-\sqrt{3}\widetilde{S}, \quad \hat{b}=\overline{X}+\sqrt{3}\widetilde{S} $$ 其中 $ =$ ,是样本二阶中心矩的开方形式 。
最大似然估计法
什么是最大似然估计法
最大似然估计(极大似然估计),是另一种点估计方法,也是机器学习等学科中经常使用到的方法。简直就是重中之重。
简单来说,就是使样本事件发生概率最大的参数值,作为总体参数的估计值,就是极大似然估计。
怎么理解呢?举个例子。
比如箱子中有100个球,共两种颜色白和黑。已知白球和黑球的比例是1:99(但不知道谁是1)。目标是估计箱子中什么颜色是99个。随机抽取一个球,发现是白球。那么从直观上讲,是不是大概率箱子中是99个白球?当然也有可能箱子中是99个黑球,正好有1个白球还正好被抽到了。但是明显这种情况概率较小。
上面这个例子,就是极大似然估计的过程。选择的是概率最大的参数。
极大似然估计的应用过程如下,也比较简单,通常遵循以下步骤
写出总体的概率/密度函数
当总体是离散型变量时,写的是概率函数;当总体是连续型函数时,写的是密度函数
写出似然函数
构造似然函数如下: $$ L(\theta) = L(x_1, x_2, \cdots, x_n ; \theta) = \prod_{i = 1}^{n} f(x_i ; \theta) $$ 从上面的公式中,其实就是将每个样本观测值带入总体概率函数中,求所有样本的概率连乘。这个连乘,就是关于总体参数的一个似然函数。
似然函数有了,下面,我们的目标就是求使得该函数取最大值时的参数值,这个参数值就将作为一个总体参数的极大似然估计。
两边取ln
由于通常似然函数都是连乘的形式,不容易取到最值,因此采用取ln的方式,将连乘变形为加法。
两边求导,令导数=0,求参数
通常情况下,最值都是在导数为0的地方取到,这里令导数=0,求参数。即此时的参数值,使得导数为0,取得整体似然函数的最大值。即,此时的参数值是整体参数的极大似然估计。
当然,如果是多个参数的情况下,这里则分别对每个参数求偏导数,令偏导数为0,分别求各个参数的极大似然估计。
具体求法
设总体X的概率密度为f(x; θ)(当X为离散型时,f(x; θ)为概率),θ = (θ1, θ2, ⋯, θk)为待估的未知参数,(x1, x2, ⋯, xn)为样本(X1, X2, ⋯, Xn)的一组观测值,称 $$ L(\theta) = L(x_1, x_2, \cdots, x_n ; \theta) = \prod_{i = 1}^{n} f(x_i ; \theta) $$ 为样本的似然函数,若存在某个θ̂ = (θ̂1, θ̂2, ⋯, θ̂k),使得 L(x1, x2, ⋯, xn; θ̂) = maxθ ∈ ΘL(x1, x2, ⋯, xn; θ) 成立(其中 Θ 为 θ 的所有可能取值范围),则称 $$ \begin{align*} \hat{\theta} &= \hat{\theta}(x_1, x_2, \cdots, x_n) \\ &= \big( \hat{\theta}_1(x_1, \cdots, x_n), \cdots, \hat{\theta}_k(x_1, \cdots, x_n) \big) \end{align*} $$ 为θ的最大似然估计值,而称 $$ \begin{align*} \hat{\theta} &= \hat{\theta}(X_1, X_2, \cdots, X_n) \\ &= \big( \hat{\theta}_1(X_1, \cdots, X_n), \cdots, \hat{\theta}_k(X_1, \cdots, X_n) \big) \end{align*} $$ 为θ的最大似然估计量。
由定义知,求总体参数 θ 的最大似然估计 θ̂ 的问题,就是求似然函数 $L() $ 的最大值问题。当然,该最大值问题解的存在性也值得关注。由微积分学知,若似然函数L(θ)关于θ(也即关于θ1, θ2, ⋯, θk)有连续偏导数,则最大似然估计θ̂ = (θ̂1, θ̂2, ⋯, θ̂k)一般可从方程组: $$ \boxed{(7.4) \quad \frac{\partial L(\theta)}{\partial \theta_j} = 0, \quad j = 1, 2, \cdots, k} $$ 解得.又由于ln L(θ)与L(θ)同时取得最大值,故等价地可由方程组 $$ \boxed{(7.5) \quad \frac{\partial \ln L(\theta)}{\partial \theta_j} = 0, \quad j = 1, 2, \cdots, k} $$
求得θ̂
(7.4)式或(7.5)式称为似然方程.通常,(7.5)式的求解较为简单.于是求解最大似然估计的一般步骤为:
由总体的分布写出样本的似然函数L(θ);
建立似然方程(7.4)式或(7.5)式;
解上述似然方程得参数θ的最大似然估计θ̂ = (θ̂1, θ̂2, ⋯, θ̂k)
例题
均匀分布的最大似然估计
设总体 X ∼ U(a, b)(均匀分布),(X1, X2, …, Xn) 为来自该总体的样本。试求参数 a 和 b 的最大似然估计(MLE)。
写出概率密度函数
均匀分布的PDF为: $$ f(x) = \begin{cases} \frac{1}{b-a} & \text{若 } a \leq x \leq b \\ 0 & \text{其他} \end{cases} $$ 构建似然函数
对于样本 (X1, X2, …, Xn),似然函数为: $$ L(a, b) = \prod_{i=1}^n f(X_i) = \begin{cases} \left(\frac{1}{b-a}\right)^n & \text{若所有 } X_i \in [a, b] \\ 0 & \text{否则} \end{cases} $$
取对数得对数似然函数 ln L(a, b) = −nln (b − a) (仅当 a ≤ Xi ≤ b 对所有 i 成立时)
最大化似然函数
由于 ln L(a, b) 关于 b − a 单调递减,因此需要 最小化 b − a,同时满足约束: $$ \begin{cases} a \leq \min(X_1, X_2, \dots, X_n), \\ b \geq \max(X_1, X_2, \dots, X_n). \end{cases} $$ 因此,MLE为: â = min (X1, X2, …, Xn), b̂ = max (X1, X2, …, Xn)
一道实际例题
某电子管的使用寿命 X
服从指数分布,其概率密度函数为
$$
f(x;\theta) = \begin{cases} \dfrac{1}{\theta} \mathrm{e}^{-x/\theta},
& x > 0, \theta > 0, \\ 0, & \text{其他}, \end{cases}
$$ 今测得一组样本观测值,其具体数据如下(单位:h):
16, 29, 50, 68, 100, 130, 140, 270, 280, 340, 410, 450, 520, 620, 190, 210, 800, 1100
试求参数 θ 的最大似然估计.
由题意,似然函数为 $$ L(x_1, x_2, \cdots, x_n ; \theta) = \prod_{i=1}^{n} \left( \dfrac{1}{\theta} \mathrm{e}^{-x_i/\theta} \right) = \dfrac{1}{\theta^n} \exp \left\{ -\dfrac{1}{\theta} \left( \sum_{i=1}^{n} x_i \right) \right\} $$ 将上式取对数得 $$ \ln L(x_1, x_2, \cdots, x_n ; \theta) = -n \ln \theta - \dfrac{1}{\theta} \sum_{i=1}^{n} x_i $$ 对 θ 求导得似然方程 $$ -\dfrac{n}{\theta} + \dfrac{1}{\theta^2} \sum_{i=1}^{n} x_i = 0 $$ 解方程得 θ 的最大似然估计值为 $$ \hat{\theta} = \dfrac{1}{n} \sum_{i=1}^{n} x_i = \bar{x}. $$ 将观测数据代入 θ̂ 中,得 θ 的最大似然估计值为 $$ \begin{align*} \hat{\theta} &= \bar{x} = \dfrac{1}{n} \sum_{i=1}^{n} x_i \\ &= \dfrac{1}{18} (16 + 29 + \cdots + 800 + 1100) = 318 \, (\text{h}). \end{align*} $$ 答,参数 θ 的最大似然估计的估计值为 318
双参指数分布的最大似然估计
设总体 X 的概率密度函数为: $$ f(x; \theta, \lambda) = \begin{cases} \lambda e^{-\lambda(x-\theta)}, & x \geq \theta \\ 0, & x < \theta \end{cases} $$ 其中 θ ∈ ℝ 和 λ > 0 是未知参数。给定样本 X1, X2, …, Xn,求 θ 和 λ 的最大似然估计量 θ̂MLE 和 λ̂MLE。
解题步骤
构造似然函数
由于样本独立同分布,似然函数为: $$ L(\theta, \lambda; x_1, x_2, \dots, x_n) = \prod_{i=1}^n \lambda e^{-\lambda(x_i - \theta)} \cdot I(x_i \geq \theta) $$ 其中 I(⋅) 是示性函数,确保所有样本点 xi ≥ θ。
当所有 xi ≥ θ 时,似然函数可简化为: $$ L(\theta, \lambda) = \lambda^n e^{-\lambda \sum_{i=1}^n (x_i - \theta)} = \lambda^n e^{-\lambda \left(\sum_{i=1}^n x_i - n\theta\right)} $$
取 ln $$ \ln L(\theta, \lambda) = n \ln \lambda - \lambda \left(\sum_{i=1}^n x_i - n\theta\right) $$ 注意:对数似然函数仅在 θ ≤ min (x1, x2, …, xn) 时有定义。
最大化关于 θ 的对数似然
ln L 中与 θ 相关的项为 nλθ,且 λ > 0。为使 ln L 最大,需让 θ 尽可能大,但必须满足 θ ≤ min (x1, x2, …, xn)。
因此,θ 的最大似然估计为: θ̂MLE = min (X1, X2, …, Xn)
最大化关于 λ 的对数似然
固定 θ = θ̂MLE,对 ln L 求导并令导数为零: $$ \frac{\partial \ln L}{\partial \lambda} = \frac{n}{\lambda} - \left(\sum_{i=1}^n x_i - n\theta\right) = 0 $$ 解得: $$ \lambda = \frac{n}{\sum_{i=1}^n x_i - n\theta} $$ 代入 θ̂MLE,得到: $$ \hat{\lambda}_{\text{MLE}} = \frac{n}{\sum_{i=1}^n X_i - n \cdot \min(X_1, X_2, \dots, X_n)} $$
最终答案 参数 θ 和 λ 的最大似然估计分别为: $$ \boxed{\hat{\theta}_{\text{MLE}} = \min(X_1, X_2, \dots, X_n)} $$ $$ \boxed{\hat{\lambda}_{\text{MLE}} = \frac{n}{\sum_{i=1}^n X_i - n \cdot \min(X_1, X_2, \dots, X_n)}} $$
估计量的评选原则
无偏性
如何理解无偏性
点估计方法判断一个点是好还是坏,涉及到的其中原则之一就是无偏性。
无偏性的含义是:用样本估计的参数值的期望,等于真实值。
通俗简单来讲,意思就是,用这个估计方法 “猜” 参数的值时,既不会系统性地高估,也不会系统性地低估,长期来看是准确的。
- 例子:假设你有一个电子秤,每次称同一块巧克力的重量时:
- 无偏的秤:有时称得重一点,有时轻一点,但 长期平均 刚好是真实重量。
- 有偏的秤:总是比真实重量多 5 克(系统性地高估)。
这个其实很好理解。我们进行参数估计不就是为了尽可能“猜”出总体参数的数值嘛,如果连期望都不相等,那岂不是基本就估计错了么……
在统计学中,“无偏估计量” 就像那个无偏的秤——用它估计参数时,虽然单次结果可能有误差,但 反复多次估计后的平均值会等于真实参数值。所以无偏估计量长期来看是准确的,避免系统性误差。
样本均值 vs 总体均值
- 用样本均值 $\bar{X} = \frac{1}{n}\sum X_i$ 估计总体均值 μ 时,X̄ 是无偏的,因为 E(X̄) = μ。
- 推断:从总体中随机抽样,样本均值会围绕真实均值波动,但不会系统性偏离。
样本方差的有偏与无偏版本
- 有偏估计:$\widetilde{S}^2 = \frac{1}{n}\sum (X_i - \bar{X})^2$,它的期望 $E(\widetilde{S}^2) = \frac{n-1}{n} \sigma^2 < \sigma^2$(低估方差)。
- 无偏估计:$S^2 = \frac{1}{n-1}\sum (X_i - \bar{X})^2$,修正后 E(S2) = σ2。
- 推断:因为 X̄ 本身是用样本数据算的,导致 S̃2 低估真实方差,需要除以 n − 1 而不是 n 来修正。
无偏性的定义
定义 7.2 设 θ̂ = θ̂(X1, X2, ⋯, Xn) 是参数 θ 的估计量,若对任意 θ ∈ Θ,有 Eθ̂ = θ 则称 θ̂ 是 θ 的无偏估计量(或称估计量 θ̂ 是无偏的)。记 bn = Eθ̂ − θ 称 bn 为估计量 θ̂ 的偏差,当 bn ≠ 0 时,称 θ̂ 是 θ 的有偏估计。若 limn → ∞bn = 0 则称 θ̂ 是 θ 的渐近无偏估计。
如何证明无偏性,来俩例题
证明样本均值$\overline X$总是总体均值EX的无偏估计量
设总体 $ X $ 的 $ k $ 阶矩 $ a_k = E(X^k) ( k )存在, (X_1, X_2, , X_n) $ 是 $ X $ 的样本。试证明样本 $ k $ 阶矩 $ A_k = _{i = 1}^n X_i^k $ 是 $ a_k $ 的无偏估计。
由样本的定义知 ( X_1, X_2, , X_n ) 与 ( X ) 同分布,因此
E(Xik) = E(Xk) = ak, k ≥ 1, i = 1, 2, ⋯, n
故 $$
EA_k = \frac{1}{n} \sum_{i = 1}^n E(X_i^k) = a_k
$$
证明$S^2 = \frac{1}{n-1}\sum (X_i - \bar{X})^2$是σ2的无偏估计量
设总体方差 $ DX = ^2 < $,试证样本方差 $ S^2 = _{i = 1}^n (X_i - {X})^2 $ 是 $ ^2 $ 的无偏估计量。
设总体均值 $ EX = $,由于 $ DX = ^2 < $,故 $ $ 存在且有限。 $$ \begin{align*} ES^2 &= E\left[ \frac{1}{n - 1} \sum_{i = 1}^n (X_i - \bar{X})^2 \right] \\ &= E\left\{ \frac{1}{n - 1} \sum_{i = 1}^n \left[ (X_i - \mu) - (\bar{X} - \mu) \right]^2 \right\} \\ &= \frac{1}{n - 1} E\left\{ \sum_{i = 1}^n \left[ (X_i - \mu)^2 - 2(X_i - \mu)(\bar{X} - \mu) + (\bar{X} - \mu)^2 \right] \right\} \\ &= \frac{1}{n - 1} \left[ \sum_{i = 1}^n E(X_i - \mu)^2 - 2E \sum_{i = 1}^n (X_i - \mu)(\bar{X} - \mu) + nE(\bar{X} - \mu)^2 \right] \\ &= \frac{1}{n - 1} \sum_{i = 1}^n E(X_i - \mu)^2 - \frac{2}{n - 1} E \sum_{i = 1}^n (X_i - \mu)(\bar{X} - \mu) + \frac{n}{n - 1} E(\bar{X} - \mu)^2 \\ &= \frac{n}{n - 1} \sigma^2 - \frac{n}{n - 1} \cdot \frac{\sigma^2}{n} \\ &= \sigma^2. \end{align*} $$ 即样本方差是总体方差的无偏估计量。
我们知道,总体方差 $ ^2 $ 的矩估计 $ ^2 = _{i = 1}^n (X_i - {X})^2 $ 是有偏估计,这是因为 $$ E\widetilde{S}^2 = E\left( \frac{n - 1}{n} S^2 \right) = \frac{n - 1}{n} ES^2 = \frac{n - 1}{n} \sigma^2 $$ 可见 $ ^2 $ 为 $ ^2 $ 的渐近无偏估计,故当 n 比较大时,取 $ S^2 $ 和 $ ^2 $ 作为 $ ^2 $ 的估计皆可。
显然,对于同一未知参数,可以构造许多无偏估计。例如,若 $ (X_1, X_2, , X_n) $ 是总体 $ X $ 的一个样本,$ c_i ( 1 i n $)是满足 $ _{i = 1}^n c_i = 1 $ 的任意常数,则估计量 $$ \sum_{i = 1}^n c_i X_i $$ 都是总体期望 EX 的无偏估计。
有效性
如何理解有效性
其实可以这么理解,有效性 衡量的是 估计量的“精度”:
- 如果两个估计量都是无偏的(长期来看都猜得准),但其中一个的估计结果 波动更小、更稳定,我们就说它 更有效。
- 类比:
- 无偏但 低效 的估计量 → 一个总是瞄准靶心但手抖的弓箭手(箭落点分散)。
- 无偏且 高效 的估计量 → 一个既瞄准靶心又手稳的弓箭手(箭密集命中靶心)。
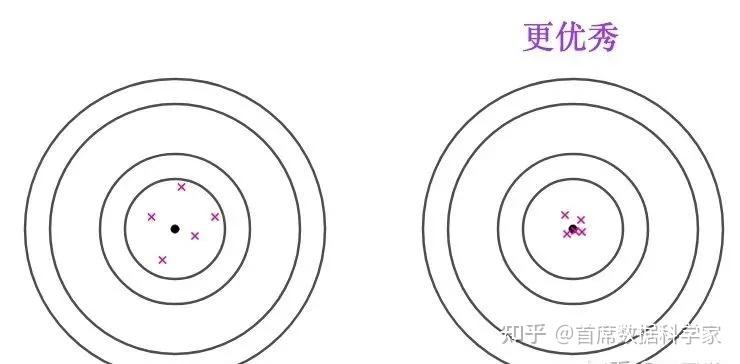
所以有效性的含义是:用样本估计的参数值的方差,如果越小,就越有效。
两个估计都是无偏的,但是第二个估计明显更集中,方差更小,因此效果也就更好。因为更加容易和真实值(即总体参数)相近。
有效性的定义
设 $\hat{\theta_1}=\hat{\theta_1}\left(X_{1}, X_{2}, \cdots, X_{n}\right)$ 和 $\hat{\theta_2}=\hat{\theta_2}\left(X_{1}, X_{2}, \cdots, X_{n}\right)$ 都是待估计参数参数 θ 的两个 无偏估计量,若: D(θ̂1) < D(θ̂2) 则称 θ̂1 比 θ̂2 更有效。
在无偏估计中,方差越小越好
方差越小 → 估计量的波动越小 → 更可能接近真实值。
有效性证明的例题
例题1:设总体服从区间 [0, θ] 上的均匀分布,(X1, X2, ⋯, Xn) 为取自该总体的容量为 n 的样本,对未知参数 θ 的两个估计量: $$ \hat{\theta}_1 = 2\bar{X}, \quad \hat{\theta}_2 = \frac{n + 1}{n} \max_{1 \leq i \leq n} \{X_i\}. $$
试验证 θ̂1 和 θ̂2 均为 θ 的无偏估计;
指出哪一个更有效。
解答: $$ E(\hat{\theta}_1) = 2E(\bar{X}) = 2 \times \frac{\theta}{2} = \theta $$
$$ E(X_{(n)}) = \int_0^\theta x \cdot \frac{n x^{n - 1}}{\theta^n} \, dx = \frac{n}{n + 1} \theta $$
$$ E(\hat{\theta}_2) = \frac{n + 1}{n} E(X_{(n)}) = \theta $$
故 θ̂1 和 θ̂2 均为 θ 的无偏估计. $$ D(\hat{\theta}_1) = 4D(\bar{X}) = \frac{4}{n^2} \sum_{i = 1}^n D(X_i) = \frac{4}{n^2} \times n \cdot \frac{\theta^2}{12} = \frac{\theta^2}{3n} $$
$$ E(X_{(n)}^2) = \int_0^\theta x^2 \cdot \frac{n x^{n - 1}}{\theta^n} \, dx = \frac{n}{n + 2} \theta^2 $$
$$ \begin{align*} D(X_{(n)}) &= E(X_{(n)}^2) - E^2(X_{(n)}) \\ &= \frac{n}{n + 2} \theta^2 - \left( \frac{n}{n + 1} \theta \right)^2 \\ &= \frac{n}{(n + 2)(n + 1)^2} \theta^2, \end{align*} $$
$$ D(\hat{\theta}_2) = \left( \frac{n + 1}{n} \right)^2 D(X_{(n)}) = \frac{\theta^2}{(n + 2)n} $$
显然当 n > 1 时,$\frac{1}{n(n + 2)} < \frac{1}{3n}$,故 θ̂2 比 θ̂1 有效
例题2:设总体 X ∼ B(1, p) 有容量为 n 的样本 (X1, X2, ⋯, Xn),其中 p ∈ (0, 1) 未知. 求 p 的无偏估计量的方差下界.
由 X 的概率分布列 f(x; p) = px(1 − p)1 − x, x = 0, 1 有 $$ \frac{\partial}{\partial p} \ln f(x; p) = \frac{\partial}{\partial p} \left[ x \ln p + (1 - x) \ln (1 - p) \right] = \frac{x}{p} - \frac{1 - x}{1 - p} = \frac{x - p}{p(1 - p)} $$ 从而 $$ \begin{align*} I(p) &= E\left( \frac{X - p}{p(1 - p)} \right)^2 \\ &= \frac{1}{p^2(1 - p)^2} E(X - p)^2 \\ &= \frac{1}{p^2(1 - p)^2} D(X) \\ &= \frac{1}{p(1 - p)}, \end{align*} $$ 此即,p 的无偏估计量方差下界为 $\frac{p(1 - p)}{n}$






