参数估计之区间估计

区间估计

什么是区间估计

上一篇文章中我们理解了什么是点估计，这次就是参数估计的另一种估计方式，区间估计。

由于点估计忽略了抽样波动性，为了更全面地反映参数估计的可靠性，我们引入区间估计

和理解点估计一样，区间估计就是估计未知参数θ的可能取值范围和这个范围包含该未知参数θ的可信程度，这个范围就是区间估计的估计内容

区间估计不仅给出一个中心点，还给出了一个上下界，使得该区间在一定的置信水平下包含真实参数值。例如，当我们计算出某总体均值的95%置信区间为[a, b]时，可以理解为在相同抽样条件下重复实验，约有95%的构造出的区间会包含总体均值。

具体说，区间估计是统计学中用来估计未知参数（比如均值、比例等）的一种方法。它不像点估计那样只给出一个具体的数值（比如“平均身高是170cm”），而是给出一个范围（比如“平均身高在168cm到172cm之间”），并说明这个范围的可信程度（比如“有95%的把握”）。

构造步骤

以单个正态总体均值的区间估计为例，构造置信区间通常包括以下步骤：

• 若总体服从正态分布，则样本均值 $\overline x$ 的抽样分布为正态分布；当总体方差未知且样本量较小时，则服从 $t $分布。

• 然后确定置信水平，

  例如设定置信水平为 95%，对应的显著性水平 α = 0.05

• 查找临界值

  当总体方差已知时，根据标准正态分布查找 z_α/2，若未知，则根据 t 分布查找，t_{n − 1; α/2}

• 构造区间

  总体均值（已知总体方差）的双侧置信区间： $$ \left( \bar{x} - z_{\alpha/2} \frac{\sigma}{\sqrt{n}},\bar{x} + z_{\alpha/2} \frac{\sigma}{\sqrt{n}} \right) $$ 总体均值（未知总体方差）的双侧置信区间：

$$ \left( \bar{x} - t_{n - 1;\alpha/2} \frac{s}{\sqrt{n}},\bar{x} + t_{n - 1;\alpha/2} \frac{s}{\sqrt{n}} \right) $$

其中 $s$ 为样本标准差，$n$ 为样本容量

置信区间与置信水平的定义

设总体 X 的分布函数为 F(x; θ)，其中 θ 是未知参数，(X₁, X₂, ⋯, X_n) 为 X 的样本。给定 α（0 < α < 1），若统计量 $\underline{\theta} = \underline{\theta}(X_1, X_2, \cdots, X_n)$ 和 $\overline{\theta} = \overline{\theta}(X_1, X_2, \cdots, X_n)$ 满足 $$ P(\underline{\theta} < \theta < \overline{\theta}) = 1 - \alpha $$ 则称区间 $(\underline{\theta}, \overline{\theta})$ 是 θ 的置信水平为 1 − α 的置信区间，$\underline{\theta}$ 和 $\overline{\theta}$ 分别称为置信下限和置信上限，1 − α 称为置信水平。

如何理解置信区间

值得注意的是，区间 $(\underline{\theta}, \overline{\theta})$ 的上、下限都是统计量，故称 $(\underline{\theta}, \overline{\theta})$ 为随机区间。随着样本观测值的不同，随机区间 $(\underline{\theta}, \overline{\theta})$ 会产生不同的具体区间。

上式$P(\underline{\theta} < \theta < \overline{\theta}) = 1 - \alpha$的意义是：

• 随机区间 $(\underline{\theta}, \overline{\theta})$ 包含 θ 真值的概率为 1 − α，而不是 θ 的真值落在区间 $(\underline{\theta}, \overline{\theta})$ 内的概率为 1 − α
• 换句话说，如果反复抽样多次（每次样本容量均为 n），每个样本观测值都会确定一个区间 $(\underline{\theta}, \overline{\theta})$，其中有的区间包含 θ 的真值，有的不包含。
• 根据伯努利大数定律，在大量重复抽样下，大约有 100(1 − α) 的区间会包含 θ 的真值，而 100α 的区间不会包含。

举例说明：

• 若 α = 0.05，反复抽样 1000 次，则大约有 950 个区间包含 θ 的真值，50 个区间不包含。
• 但对于某一个具体的区间（如某次抽样得到的 [a, b]），我们不能说“θ 有 95 的概率落在这个区间内”，因为 θ 是固定值，只能说“这个区间属于那些有 95 置信度包含 θ 的区间之一”。

感觉说的依旧不太清晰，我重新说一下

什么是随机区间？

• $\underline{\theta}$ 和 $\overline{\theta}$ 是由样本计算得到的统计量（如样本均值X̄、样本标准差S等），因此 $(\underline{\theta}, \overline{\theta})$ 是一个随机区间（每次抽样结果不同）。
• 举例： 假设我们估计全校学生的平均身高μ，每次随机抽100人计算：
  • 第1次抽样：X̄₁ = 168，得到区间(165, 171)
  • 第2次抽样：X̄₂ = 170，得到区间(167, 173)
  • … 这些区间会因样本不同而变化，但大约95的区间会包含真实μ（假设置信水平1 − α = 95）。

置信水平1 − α的含义

• 正确理解：

  $P(\underline{\theta} < \theta < \overline{\theta}) = 1-\alpha$ 表示：

  在无数次重复抽样中，100(1 − α)的区间会覆盖真实参数θ，而不是θ有1 − α的概率落在当前区间内（因为θ是固定值，不是随机变量）。

• 类比： 想象你用渔网（置信区间）捞鱼（真实参数θ）：

  • 如果渔网有95的捕获率（1 − α = 0.95），意味着长期来看，撒网100次大约有95次能捞到鱼。
  • 但某一次撒网后，鱼要么在网里（100%），要么不在（0%），不能说“鱼有95%的概率在网里”。

举例说明（α = 0.05）

• 重复抽样100次： 理论上，大约95次计算出的区间会包含真实θ，5次不包含。

  • 例如：估计某药品的有效率θ，100次实验得到95个区间包含真实值（如(0.6, 0.8)），5个区间不包含（如(0.4, 0.6)）。

• 单次区间的解释： 如果你得到一个具体区间(0.65, 0.75)，只能说：

  “这个区间是通过一个方法生成的，而该方法有95的可靠性覆盖真实值”， 而不是“θ有95的概率在(0.65, 0.75)内”。

为什么不能对单个区间谈概率？

• θ是固定参数（如全校平均身高μ = 169cm），而区间是随机的。
• 类比： 你测量一块石头的重量θ，用天平测10次得到10个区间。
  • 石头重量θ是固定的，但测量区间会波动。
  • 只能说“我的测量方法有95的置信度包含真实重量”，而不是“θ有95的概率在某个区间内”。

单个正态总体的区间估计

我们主要介绍枢轴量法，统计量法懒得写了

单个正态总体均值的区间估计

设已给定置信水平为 1 − α, 并设 (X₁, X₂, ⋯, X_n) 是总体 N(μ, σ²) 的样本. X̄ 和 S² 分别是样本均值和样本方差. 对总体均值作区间估计, 分总体方差 σ² 已知和未知两种情况.

σ² 已知

推导步骤

首先构建统计量

样本均值$\bar{X} = \frac{1}{n}\sum_{i=1}^n X_i$服从正态分布，所以随机变量 $$ \bar{X} \sim N\left(\mu, \frac{\sigma^2}{n}\right) $$

将其标准化得到U统计量： $$ U = \frac{\bar{X} - \mu}{\sigma/\sqrt{n}} \sim N(0,1) $$

对于给定的显著性水平α，查标准正态分布表得到u_α/2，满足： $$ P\left( |U| \geq u_{\frac{\alpha}{2}} \right) = P\left( \left| \frac{\bar{X} - \mu}{\sigma} \sqrt{n} \right| \geq u_{\frac{\alpha}{2}} \right) = \alpha \tag{7.9} $$

image-20250626094043358

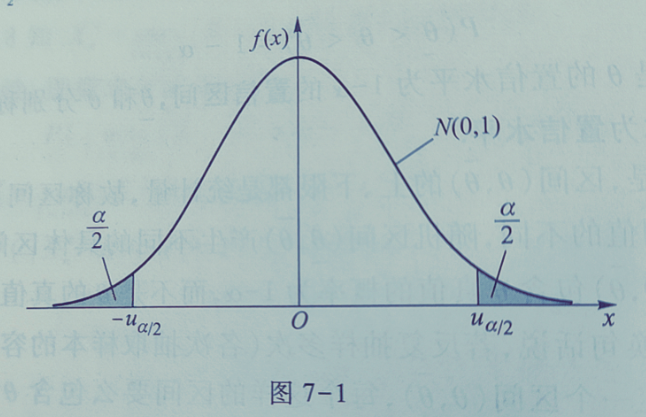
等价于： P(−u_α/2 ≤ U ≤ u_α/2) = 1 − α

将U的表达式代入： $$ P\left(-u_{\alpha/2} \leq \frac{\bar{X} - \mu}{\sigma/\sqrt{n}} \leq u_{\alpha/2}\right) = 1 - \alpha $$

解这个不等式：

1. 两边乘以$\sigma/\sqrt{n}$： $$ P\left(-\frac{\sigma}{\sqrt{n}}u_{\alpha/2} \leq \bar{X} - \mu \leq \frac{\sigma}{\sqrt{n}}u_{\alpha/2}\right) = 1 - \alpha $$

2. 移项得到μ的范围： $$ P\left(\bar{X} - \frac{\sigma}{\sqrt{n}}u_{\alpha/2} \leq \mu \leq \bar{X} + \frac{\sigma}{\sqrt{n}}u_{\alpha/2}\right) = 1 - \alpha $$

所以，(7.9) 式等价于 $$ P\left( \bar{X} - \frac{\sigma}{\sqrt{n}} u_{\alpha/2} < \mu < \bar{X} + \frac{\sigma}{\sqrt{n}} u_{\alpha/2} \right) = 1 - \alpha, $$ 由此得到 μ 的置信水平为 1 − α (简称 1 − α) 的置信区间为 $$ \left( \bar{X} - \frac{\sigma}{\sqrt{n}} u_{\alpha/2},\ \bar{X} + \frac{\sigma}{\sqrt{n}} u_{\alpha/2} \right). \tag{7.10} $$

实际计算步骤

1. 计算样本均值： $$ \bar{x} = \frac{1}{n}\sum_{i=1}^n x_i $$

2. 查表得到u_α/2值（例如α = 0.05时，u_0.025 = 1.96）

3. 代入公式计算上下限：

   • 下限：$\bar{x} - \frac{\sigma}{\sqrt{n}}u_{\alpha/2}$
   • 上限：$\bar{x} + \frac{\sigma}{\sqrt{n}}u_{\alpha/2}$

σ² 未知

推导过程

此时不能采用上面的式子给出的区间，因为其中含未知参数 σ。

由于 S² 是 σ²的无偏估计，当总体方差σ²未知时，无法直接使用Z统计量： $$ Z = \frac{\bar{X} - \mu}{\sigma/\sqrt{n}} \sim N(0,1) $$ 因为公式中含未知参数σ。

所以，用样本标准差S替代σ，构造t统计量： $$ t = \frac{\bar{X} - \mu}{S/\sqrt{n}} \sim t(n-1) $$ 其中： - $S^2 = \frac{1}{n-1}\sum_{i=1}^n (X_i - \bar{X})^2$是样本方差 - t(n − 1)表示自由度为n − 1的t分布

确定临界值

对给定 α(0 < α < 1), 查 t 分布表, 可得 t(n − 1) 分布的双侧分位数 t_α/2(n − 1), 使得 P(|t| ≥ t_α/2(n − 1)) = α 即： P(|t| < t_α/2(n − 1)) = 1 − α

P(−t_α/2(n − 1) < t < t_α/2(n − 1)) = 1 − α

image-20250626100334605

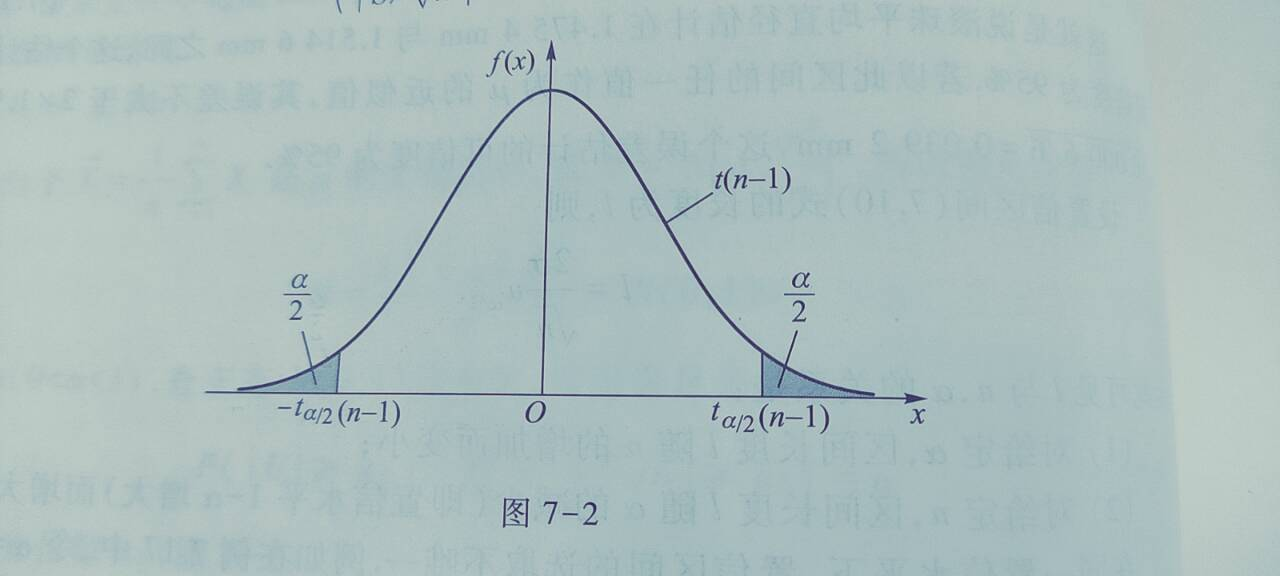
现在就可以开始具体的置信区间的推导了

将t统计量表达式代入： $$ P\left(-t_{\alpha/2}(n-1) < \frac{\bar{X} - \mu}{S/\sqrt{n}} < t_{\alpha/2}(n-1)\right) = 1 - \alpha $$

逐步解这个不等式： 1. 乘以$S/\sqrt{n}$： $$ P\left(-\frac{S}{\sqrt{n}}t_{\alpha/2}(n-1) < \bar{X} - \mu < \frac{S}{\sqrt{n}}t_{\alpha/2}(n-1)\right) = 1 - \alpha $$

2. 移项得到μ的范围： $$ P\left(\bar{X} - \frac{S}{\sqrt{n}}t_{\alpha/2}(n-1) < \mu < \bar{X} + \frac{S}{\sqrt{n}}t_{\alpha/2}(n-1)\right) = 1 - \alpha $$

最终，μ的置信水平为1 − α的置信区间为： $$ \left( \bar{X} - \frac{S}{\sqrt{n}}t_{\alpha/2}(n-1),\ \bar{X} + \frac{S}{\sqrt{n}}t_{\alpha/2}(n-1) \right) $$

实际上计算步骤

1. 计算样本统计量： $$ \bar{x} = \frac{1}{n}\sum_{i=1}^n x_i,\quad s = \sqrt{\frac{1}{n-1}\sum_{i=1}^n (x_i - \bar{x})^2} $$

2. 查t分布表得临界值t_α/2(n − 1)

3. 计算置信区间：

   • 下限：$\bar{x} - \frac{s}{\sqrt{n}}t_{\alpha/2}(n-1)$
   • 上限：$\bar{x} + \frac{s}{\sqrt{n}}t_{\alpha/2}(n-1)$

单个正态总体方差的区间估计

μ 未知

设总体 X ∼ N(μ, σ²)，(X₁, X₂, ⋯, X_n) 是 X 的样本。对总体方差 σ² 作区间估计，同样分成 μ 已知和未知两种情形。

此处，根据实际情况的需要，只讨论 μ 未知的情况。

设总体X ∼ N(μ, σ²)，样本为(X₁, X₂, ⋯, X_n)，置信水平为1 − α。

为什么根据实际情况的需要这里只讨论μ 未知的情况

• 因为在绝大多数实际问题中，总体均值μ和方差σ²同时未知才是常态。例如：
  • 测量某零件的尺寸误差（μ和σ²均需估计）
  • 分析某地区居民收入分布（均值和方差都需要从样本推断）
• μ已知的情况在现实中非常罕见（除非进行仿真实验或理论推导）
• μ已知的情况可通过替换X̄→μ直接推导

推导过程

首先先构造统计量

由样本方差$S^2 = \frac{1}{n-1}\sum_{i=1}^n (X_i - \bar{X})^2$，构造卡方统计量： $$ \chi^2 = \frac{(n-1)S^2}{\sigma^2} \sim \chi^2(n-1) $$

确定临界值

对于给定的α，查χ²分布表得： - 下侧分位数χ_{1 − α/2}²(n − 1) - 上侧分位数χ_α/2²(n − 1)

满足： $$ P\left(\chi^2_{1-\alpha/2}(n-1) < \frac{(n-1)S^2}{\sigma^2} < \chi^2_{\alpha/2}(n-1)\right) = 1-\alpha $$

image-20250626101211666

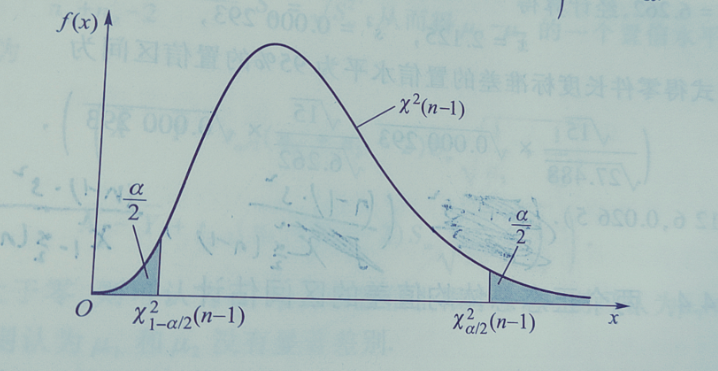
推导置信区间

解不等式： 1. 不等式变形： $$ \chi^2_{1-\alpha/2}(n-1) < \frac{(n-1)S^2}{\sigma^2} < \chi^2_{\alpha/2}(n-1) $$

2. 取倒数（注意不等号方向变化）： $$ \frac{1}{\chi^2_{1-\alpha/2}(n-1)} > \frac{\sigma^2}{(n-1)S^2} > \frac{1}{\chi^2_{\alpha/2}(n-1)} $$

3. 乘以(n − 1)S²： $$ \frac{(n-1)S^2}{\chi^2_{1-\alpha/2}(n-1)} > \sigma^2 > \frac{(n-1)S^2}{\chi^2_{\alpha/2}(n-1)} $$

而且χ_α/2²(n − 1)和χ_{1 − α/2}²(n − 1)的值都可以通过查χ²(n − 1)的分布表得到

所以有 $$ P\left( \frac{(n - 1)S^2}{\chi^2_{\alpha/2}(n - 1)} < \sigma^2 < \frac{(n - 1)S^2}{\chi^2_{1 - \alpha/2}(n - 1)} \right) = 1 - \alpha. $$ 因此方差σ²的一个置信水平为1 − α的置信区间为： $$ \left( \frac{(n-1)S^2}{\chi^2_{\alpha/2}(n-1)},\ \frac{(n-1)S^2}{\chi^2_{1-\alpha/2}(n-1)} \right) $$

对σ²区间取平方根，可以得到标准差σ的一个置信水平为1 − α的置信区间 $$ \left( \frac{\sqrt{n-1}S}{\sqrt{\chi^2_{\alpha/2}(n-1)}},\ \frac{\sqrt{n-1}S}{\sqrt{\chi^2_{1-\alpha/2}(n-1)}} \right) $$

实际计算步骤

1. 计算样本方差： $$ s^2 = \frac{1}{n-1}\sum_{i=1}^n (x_i - \bar{x})^2 $$

2. 查χ²分布表：

   • χ_α/2²(n − 1)（右侧临界值）
   • χ_{1 − α/2}²(n − 1)（左侧临界值）

3. 计算置信区间：

   • 方差区间： $$ \left( \frac{(n-1)s^2}{\chi^2_{\alpha/2}(n-1)},\ \frac{(n-1)s^2}{\chi^2_{1-\alpha/2}(n-1)} \right) $$
   • 标准差区间： $$ \left( \sqrt{\frac{(n-1)s^2}{\chi^2_{\alpha/2}(n-1)}},\ \sqrt{\frac{(n-1)s^2}{\chi^2_{1-\alpha/2}(n-1)}} \right) $$

μ 已知

想了一下μ已知的情况，也算一下得了，要不然总感觉怪怪的

设总体X ∼ N(μ, σ²)，其中μ已知，(X₁, X₂, ⋯, X_n)为样本，置信水平为1 − α。

推导过程

构建统计量

定义真实离差平方和： $$ Q = \sum_{i=1}^n (X_i - \mu)^2 $$

由于X_i ∼ N(μ, σ²)，标准化后有： $$ \frac{X_i - \mu}{\sigma} \sim N(0,1) \quad \Rightarrow \quad \left(\frac{X_i - \mu}{\sigma}\right)^2 \sim \chi^2(1) $$

根据卡方分布的可加性： $$ \chi^2 = \frac{Q}{\sigma^2} = \sum_{i=1}^n \left(\frac{X_i - \mu}{\sigma}\right)^2 \sim \chi^2(n) $$

确定临界值

对于给定的α，查χ²分布表得：

• 下侧分位数χ_{1 − α/2}²(n)
• 上侧分位数χ_α/2²(n)

满足概率等式： $$ P\left(\chi^2_{1-\alpha/2}(n) < \frac{Q}{\sigma^2} < \chi^2_{\alpha/2}(n)\right) = 1-\alpha $$

推导置信区间 解关于σ²的不等式：

1. 原始不等式： $$ \chi^2_{1-\alpha/2}(n) < \frac{\sum (X_i - \mu)^2}{\sigma^2} < \chi^2_{\alpha/2}(n) $$

2. 取倒数（注意不等号方向变化）： $$ \frac{1}{\chi^2_{1-\alpha/2}(n)} > \frac{\sigma^2}{\sum (X_i - \mu)^2} > \frac{1}{\chi^2_{\alpha/2}(n)} $$

3. 乘以∑(X_i − μ)²： $$ \frac{\sum (X_i - \mu)^2}{\chi^2_{1-\alpha/2}(n)} > \sigma^2 > \frac{\sum (X_i - \mu)^2}{\chi^2_{\alpha/2}(n)} $$

因此σ²的置信区间为： $$ \left( \frac{\sum_{i=1}^n (X_i - \mu)^2}{\chi^2_{\alpha/2}(n)},\ \frac{\sum_{i=1}^n (X_i - \mu)^2}{\chi^2_{1-\alpha/2}(n)} \right) $$

对σ²区间取平方根，就可以得到标准差σ的置信区间： $$ \left( \sqrt{\frac{\sum (X_i - \mu)^2}{\chi^2_{\alpha/2}(n)}},\ \sqrt{\frac{\sum (X_i - \mu)^2}{\chi^2_{1-\alpha/2}(n)}} \right) $$

实际计算步骤

设μ = 5，样本观测值(4.8, 5.1, 4.9, 5.2, 5.0)，α = 0.05：

1. 计算离差平方和： ∑(x_i − 5)² = 0.10

2. 查χ²分布表（n = 5）：

   • χ_0.025²(5) = 12.833
   • χ_0.975²(5) = 0.831

3. 方差置信区间： $$ \left( \frac{0.10}{12.833},\ \frac{0.10}{0.831} \right) = (0.0078,\ 0.1203) $$

4. 标准差置信区间： $$ \left( \sqrt{0.0078},\ \sqrt{0.1203} \right) = (0.088,\ 0.347) $$

两个正态总体均值差的区间估计

设已给定置信水平为 1 − α，并设 (X₁, X₂, ⋯, X_n1) 是总体 X ∼ N(μ₁, σ₁²) 的样本，(Y₁, Y₂, ⋯, Y_n2) 是总体 Y ∼ N(μ₂, σ₂²) 的样本，且这两个样本相互独立。

记 X̄, Ȳ 分别是总体 X 和 Y 的样本均值，S₁², S₂² 分别是总体 X 和 Y 的样本方差。对总体均值差 μ₁ − μ₂ 作区间估计，分如下三种情况讨论。

σ₁²和σ₂²均已知

推导过程

无偏估计量的构造

由于： - X̄是μ₁的无偏估计：E(X̄) = μ₁ - Ȳ是μ₂的无偏估计：E(Ȳ) = μ₂

因此： D = X̄ − Ȳ  是  δ = μ₁ − μ₂  的无偏估计

由正态分布性质： $$ \begin{aligned} \bar{X} &\sim N\left(\mu_1, \frac{\sigma_1^2}{n_1}\right) \\ \bar{Y} &\sim N\left(\mu_2, \frac{\sigma_2^2}{n_2}\right) \end{aligned} $$

由于X̄与Ȳ相互独立，其线性组合服从： $$ \bar{X} - \bar{Y} \sim N\left(\mu_1 - \mu_2, \frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}\right) $$

标准化统计量，构造标准正态统计量：

$$ U = \frac{(\bar{X} - \bar{Y}) - (\mu_1 - \mu_2)}{\sqrt{\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}}} \sim N(0,1) $$

置信区间推导

对于给定α，查标准正态分布得u_α/2满足： P(−u_α/2 < U < u_α/2) = 1 − α

将U表达式代入： $$ P\left(-u_{\alpha/2} < \frac{D - \delta}{\sqrt{\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}}} < u_{\alpha/2}\right) = 1 - \alpha $$

解不等式： 1. 乘以标准差： $$ P\left(-u_{\alpha/2}\sqrt{\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}} < D - \delta < u_{\alpha/2}\sqrt{\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}}\right) = 1 - \alpha $$

2. 移项得： $$ P\left(D - u_{\alpha/2}\sqrt{\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}} < \delta < D + u_{\alpha/2}\sqrt{\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}}\right) = 1 - \alpha $$

最终置信区间

μ₁ − μ₂的1 − α置信区间为： $$ \left( \bar{X} - \bar{Y} - u_{\alpha/2}\sqrt{\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}},\ \bar{X} - \bar{Y} + u_{\alpha/2}\sqrt{\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}} \right) $$

实际计算步骤

1. 计算样本均值： $$ \bar{x} = \frac{1}{n_1}\sum x_i,\quad \bar{y} = \frac{1}{n_2}\sum y_i $$

2. 查标准正态分布表得u_α/2值：

   • α = 0.05时，u_0.025 = 1.96

3. 计算合并标准误： $$ SE = \sqrt{\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}} $$

4. 计算置信区间： CI = (x̄ − ȳ) ± 1.96 × SE

示例：

设n₁ = 30, σ₁² = 4, x̄ = 10.2
n₂ = 40, σ₂² = 9, ȳ = 8.5, α = 0.05

1. 计算标准误： $$ SE = \sqrt{\frac{4}{30} + \frac{9}{40}} = \sqrt{0.1333 + 0.225} = 0.598 $$

2. 置信区间： (10.2 − 8.5) ± 1.96 × 0.598 = 1.7 ± 1.172 = (0.528, 2.872)

σ₁²和σ₂²均未知，但是σ₁² = σ₂² = σ²

推导过程

合并方差估计

构造合并方差估计量： $$ S_w^2 = \frac{(n_1-1)S_1^2 + (n_2-1)S_2^2}{n_1+n_2-2} $$

• 分子：两样本离差平方和的加权组合
• 分母：总自由度df = n₁ + n₂ − 2

构建t统计量

标准化均值差： $$ T = \frac{(\bar{X} - \bar{Y}) - (\mu_1 - \mu_2)}{S_w \sqrt{\frac{1}{n_1} + \frac{1}{n_2}}} \sim t(n_1+n_2-2) $$

而其中，S_w为 $$ S_w^2 = \frac{(n_1-1)S_1^2 + (n_2-1)S_2^2}{n_1+n_2-2} $$ 置信区间推导

对于给定α，查t分布表得t_α/2(df)满足： P(−t_α/2(df) < T < t_α/2(df)) = 1 − α

展开后得到： $$ P\left(\bar{X}-\bar{Y} - t_{\alpha/2} S_w \sqrt{\frac{1}{n_1} + \frac{1}{n_2}} < \mu_1 - \mu_2 < \bar{X}-\bar{Y} + t_{\alpha/2} S_w \sqrt{\frac{1}{n_1} + \frac{1}{n_2}}\right) = 1 - \alpha $$

整理得到置信区间公式

μ₁ − μ₂的一个置信水平为1 − α的置信区间： $$ \left(\bar{X} - \bar{Y} - t_{\alpha/2}(n_1+n_2-2) \cdot S_w \sqrt{\frac{1}{n_1} + \frac{1}{n_2}}, \bar{X} - \bar{Y} + t_{\alpha/2}(n_1+n_2-2) \cdot S_w \sqrt{\frac{1}{n_1} + \frac{1}{n_2}}\right) $$

实际计算步骤

1. 计算样本统计量： $$ \bar{x} = \frac{1}{n_1}\sum x_i,\quad s_1^2 = \frac{1}{n_1-1}\sum(x_i-\bar{x})^2 \\ \bar{y} = \frac{1}{n_2}\sum y_i,\quad s_2^2 = \frac{1}{n_2-1}\sum(y_i-\bar{y})^2 $$

2. 计算合并方差： $$ s_w^2 = \frac{(n_1-1)s_1^2 + (n_2-1)s_2^2}{n_1+n_2-2} $$

3. 查t分布表得临界值t_α/2(n₁ + n₂ − 2)

4. 计算置信区间： $$ \text{CI} = (\bar{x} - \bar{y}) \pm t_{\alpha/2} \cdot s_w \sqrt{\frac{1}{n_1} + \frac{1}{n_2}} $$

示例计算

设n₁ = 15, x̄ = 50.2, s₁² = 16
n₂ = 20, ȳ = 48.5, s₂² = 12.5, α = 0.05

1. 计算合并方差： $$ s_w^2 = \frac{14\times16 + 19\times12.5}{33} = \frac{224 + 237.5}{33} \approx 14.0 $$

2. 查t分布表：

   t_0.025(33) ≈ 2.0345

3. 计算置信区间： $$ 1.7 \pm 2.0345 \times \sqrt{14} \times \sqrt{\frac{1}{15} + \frac{1}{20}} \\ = 1.7 \pm 2.0345 \times 3.7417 \times 0.3416 \\ = 1.7 \pm 2.60 \\ = (-0.90, 4.30) $$

4. 结论：区间包含0，不能认为μ₁与μ₂有显著差异

σ₁²和σ₂²均未知，但是关系不确定

推导过程

设两独立总体： - X ∼ N(μ₁, σ₁²)，样本(X₁, ..., X_n1)，样本均值X̄，样本方差S₁² - Y ∼ N(μ₂, σ₂²)，样本(Y₁, ..., Y_n2)，样本均值Ȳ，样本方差S₂²

构建统计量

考虑均值差δ = μ₁ − μ₂的估计量： $$ D = \bar{X} - \bar{Y} \sim N\left(\delta, \frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}\right) $$

标准化后： $$ T = \frac{D - \delta}{\sqrt{\frac{S_1^2}{n_1} + \frac{S_2^2}{n_2}}} \sim t(\nu) $$ 其中自由度ν由Welch-Satterthwaite方程确定：

自由度计算

$$ \nu = \frac{\left(\frac{S_1^2}{n_1} + \frac{S_2^2}{n_2}\right)^2}{\frac{(S_1^2/n_1)^2}{n_1-1} + \frac{(S_2^2/n_2)^2}{n_2-1}} $$

置信区间推导

对于给定α，查t分布表得t_α/2(ν)，满足： $$ P\left(-t_{\alpha/2}(\nu) < \frac{(\bar{X}-\bar{Y}) - (\mu_1-\mu_2)}{\sqrt{\frac{S_1^2}{n_1} + \frac{S_2^2}{n_2}}} < t_{\alpha/2}(\nu)\right) = 1-\alpha $$

解不等式得δ的置信区间： $$ (\bar{X}-\bar{Y}) \pm t_{\alpha/2}(\nu)\sqrt{\frac{S_1^2}{n_1} + \frac{S_2^2}{n_2}} $$

计算步骤

1. 计算样本统计量： $$ \bar{x} = \frac{1}{n_1}\sum x_i,\quad s_1^2 = \frac{1}{n_1-1}\sum(x_i-\bar{x})^2 \\ \bar{y} = \frac{1}{n_2}\sum y_i,\quad s_2^2 = \frac{1}{n_2-1}\sum(y_i-\bar{y})^2 $$

2. 计算自由度ν（结果四舍五入取整）： $$ \nu = \frac{\left(\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}\right)^2}{\frac{(s_1^2/n_1)^2}{n_1-1} + \frac{(s_2^2/n_2)^2}{n_2-1}} $$

3. 查t分布表得临界值t_α/2(ν)

4. 计算置信区间： $$ \text{CI} = (\bar{x}-\bar{y}) \pm t_{\alpha/2}(\nu)\sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}} $$

实际计算步骤

设n₁ = 10, x̄ = 5.2, s₁² = 1.5 ，n₂ = 15, ȳ = 4.8, s₂² = 2.0, α = 0.05

1. 计算自由度： $$ \nu = \frac{(0.15+0.1333)^2}{0.0225/9 + 0.0178/14} \approx 21.3 \approx 21 $$

2. 查t_0.025(21) = 2.080

3. 置信区间： $$ 0.4 \pm 2.080\sqrt{0.15+0.1333} = 0.4 \pm 2.080\times0.532 = (-0.706, 1.506) $$

两个正态总体方差比的区间估计

设 (X₁, X₂, ⋯, X_n1) 是总体 X ∼ N(μ₁, σ₁²) 的样本，(Y₁, Y₂, ⋯, Y_n2) 是总体 Y ∼ N(μ₂, σ₂²) 的样本，且两个样本相互独立，要求两总体方差比 σ₁²/σ₂² 的置信水平为 (1 − α) 的置信区间。

μ₁,μ₂均未知的情况

推导过程

构建F统计量

由抽样分布理论： $$ F = \frac{S_1^2/\sigma_1^2}{S_2^2/\sigma_2^2} \sim F(n_1-1, n_2-1) $$

且分布 F(n₁ − 1, n₂ − 1) 不依赖任何参数. 由 F 分布的上侧分位数的定义知

image-20250626104603082

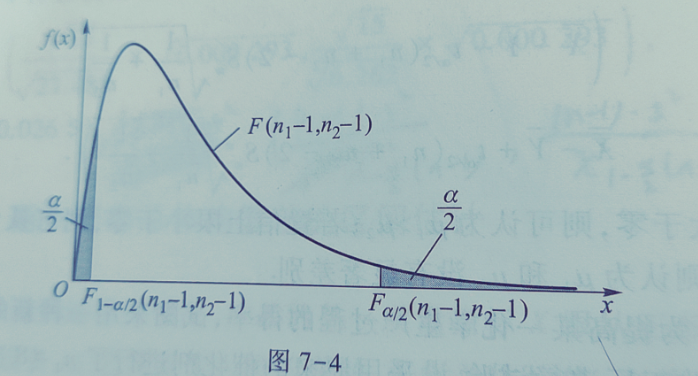
确定临界值

对于给定α，查F分布表得： - 上侧分位数F_α/2(n₁ − 1, n₂ − 1) - 下侧分位数F_{1 − α/2}(n₁ − 1, n₂ − 1)

满足概率等式： $$ P\left(F_{1-\alpha/2} < \frac{S_1^2/\sigma_1^2}{S_2^2/\sigma_2^2} < F_{\alpha/2}\right) = 1-\alpha $$

推导置信区间

解关于σ₁²/σ₂²的不等式：

1. 原始不等式： $$ F_{1-\alpha/2} < \frac{S_1^2}{S_2^2} \cdot \frac{\sigma_2^2}{\sigma_1^2} < F_{\alpha/2} $$

2. 取倒数（注意不等号方向变化）： $$ \frac{1}{F_{1-\alpha/2}} > \frac{S_2^2}{S_1^2} \cdot \frac{\sigma_1^2}{\sigma_2^2} > \frac{1}{F_{\alpha/2}} $$

3. 乘以$\frac{S_1^2}{S_2^2}$： $$ \frac{S_1^2}{S_2^2} \cdot \frac{1}{F_{\alpha/2}} < \frac{\sigma_1^2}{\sigma_2^2} < \frac{S_1^2}{S_2^2} \cdot \frac{1}{F_{1-\alpha/2}} $$

最终置信区间

σ₁²/σ₂²的1 − α置信区间： $$ \left( \frac{S_1^2}{S_2^2} \cdot \frac{1}{F_{\alpha/2}(n_1-1,n_2-1)},\ \frac{S_1^2}{S_2^2} \cdot \frac{1}{F_{1-\alpha/2}(n_1-1,n_2-1)} \right) $$

实际计算步骤

1. 计算样本方差： $$ s_1^2 = \frac{1}{n_1-1}\sum(x_i-\bar{x})^2,\quad s_2^2 = \frac{1}{n_2-1}\sum(y_i-\bar{y})^2 $$

2. 计算方差比： $$ \frac{s_1^2}{s_2^2} $$

3. 查F分布表：

   • F_α/2(df₁, df₂)
   • $F_{1-\alpha/2}(df_1,df_2) = \frac{1}{F_{\alpha/2}(df_2,df_1)}$

4. 计算置信区间：

   • 下限：$\frac{s_1^2}{s_2^2} \cdot \frac{1}{F_{\alpha/2}(n_1-1,n_2-1)}$
   • 上限：$\frac{s_1^2}{s_2^2} \cdot \frac{1}{F_{1-\alpha/2}(n_1-1,n_2-1)}$

示例

设n₁ = 10, s₁² = 4.5
n₂ = 15, s₂² = 2.8, α = 0.05

1. 计算方差比： $$ \frac{4.5}{2.8} \approx 1.607 $$

2. 查F分布表：

   • F_0.025(9, 14) = 3.209
   • $F_{0.975}(9,14) = \frac{1}{F_{0.025}(14,9)} = \frac{1}{3.798} \approx 0.263$

3. 置信区间：

   • 下限：$1.607 \times \frac{1}{3.209} \approx 0.501$
   • 上限：$1.607 \times \frac{1}{0.263} \approx 6.110$ (0.501, 6.110)

μ₁已知，μ₂未知

推导过程

1. 构建统计量： 当μ₁已知时，使用真实离差构造样本方差： $$ S_1^{*2} = \frac{1}{n_1}\sum_{i=1}^{n_1}(X_i - \mu_1)^2 \sim \frac{\sigma_1^2}{n_1}\chi^2(n_1) $$ 而S₂²仍为常规样本方差： $$ S_2^2 = \frac{1}{n_2-1}\sum_{i=1}^{n_2}(Y_i - \bar{Y})^2 \sim \frac{\sigma_2^2}{n_2-1}\chi^2(n_2-1) $$

2. 构造F统计量： $$ F = \frac{S_1^{*2}/\sigma_1^2}{S_2^2/\sigma_2^2} \sim F(n_1, n_2-1) $$

3. 确定临界值： 查F分布表得F_α/2(n₁, n₂ − 1)和F_{1 − α/2}(n₁, n₂ − 1)

4. 推导置信区间： $$ \left( \frac{S_1^{*2}}{S_2^2} \cdot \frac{1}{F_{\alpha/2}(n_1,n_2-1)},\ \frac{S_1^{*2}}{S_2^2} \cdot \frac{1}{F_{1-\alpha/2}(n_1,n_2-1)} \right) $$

示例计算

设μ₁ = 5, n₁ = 10, ∑(x_i − 5)² = 40
n₂ = 15, s₂² = 3.2, α = 0.05

1. 计算S₁^*2 = 40/10 = 4
2. 方差比：4/3.2 = 1.25
3. 查F分布表：
   • F_0.025(10, 14) = 3.15
   • F_0.975(10, 14) = 1/F_0.025(14, 10) ≈ 1/3.35 ≈ 0.299
4. 置信区间：
   • 下限：1.25 × 1/3.15 ≈ 0.397
   • 上限：1.25 × 1/0.299 ≈ 4.181

μ₁,μ₂均已知

推导过程

1. 构建统计量： 使用真实离差构造方差估计： $$ S_1^{*2} = \frac{1}{n_1}\sum(X_i - \mu_1)^2 \sim \frac{\sigma_1^2}{n_1}\chi^2(n_1) \\ S_2^{*2} = \frac{1}{n_2}\sum(Y_i - \mu_2)^2 \sim \frac{\sigma_2^2}{n_2}\chi^2(n_2) $$

2. 构造F统计量： $$ F = \frac{S_1^{*2}/\sigma_1^2}{S_2^{*2}/\sigma_2^2} \sim F(n_1, n_2) $$

3. 确定临界值：

   查F分布表得F_α/2(n₁, n₂)和F_{1 − α/2}(n₁, n₂)

4. 推导置信区间： $$ \left( \frac{S_1^{*2}}{S_2^{*2}} \cdot \frac{1}{F_{\alpha/2}(n_1,n_2)},\ \frac{S_1^{*2}}{S_2^{*2}} \cdot \frac{1}{F_{1-\alpha/2}(n_1,n_2)} \right) $$

示例计算

设μ₁ = 5, μ₂ = 6, n₁ = 8, ∑(x_i − 5)² = 24
n₂ = 12, ∑(y_i − 6)² = 42, α = 0.1

1. 计算方差估计：
   • S₁^*2 = 24/8 = 3
   • S₂^*2 = 42/12 = 3.5
2. 方差比：3/3.5 ≈ 0.857
3. 查F分布表：
   • F_0.05(8, 12) = 2.85
   • F_0.95(8, 12) = 1/F_0.05(12, 8) ≈ 1/3.28 ≈ 0.305
4. 置信区间：
   • 下限：0.857 × 1/2.85 ≈ 0.301
   • 上限：0.857 × 1/0.305 ≈ 2.810