随机变量的假设检验

假设检验

什么是参数的假设检验

参数的假设检验通常是指，根据样本来判断总体分布的数字特征是否是某一个指定的数。

例如，已知样本来着正态总体N(μ, σ²)，要判断它是否来自均值μ = μ₀，方差σ² = σ₀²的正态总体，这里μ₀和σ₀²是已知数。

所以，假设检验就像一场“辩论”，目的是用数据判断某个关于总体参数的假设（比如“平均值等于5”）是否成立。所以假设检验的逻辑是我先做一个假设，然后看数据结果是足够反驳它还是足够接受他，如果数据非常不支持，就拒绝这个假设。

所以做假设检验时会设置两个假设：

原假设（H₀）(零假设)：默认的、保守的假设（比如“均值=5”或“新药=旧药”）。
备择假设（H₁）：你想证明的结论（比如“均值≠5”或“新药>旧药”）。

然后，根据数据类型（均值、比例等）选一个公式计算统计量（比如t值、z值），用来衡量数据与原假设的差距。之后确定显著性水平，通常选α = 0.05，表示“如果H₀成立，只有5%的概率会误判拒绝它”（即容忍的犯错风险）。最后根据结果判断结论

这样，问题转化为检验假设H₀是否为真（成立），当H₀为真，则接受假设，否则不接受

具体一个例子说明：

味精厂用一台包装机自动包装味精，包得的袋装味精质量服从 N(μ, σ²)。当机器正常时,其均值 μ₀ = 0.5 kg,标准差 σ₀ = 0.015 kg.某日开工后随机地抽取 9 袋味精，称得质量(单位:kg)为：0.497, 0.506, 0.518, 0.524, 0.498, 0.511, 0.520, 0.515, 0.512,问这台包装机是否正常?

根据实际问题，若 X 表示袋装味精的质量,则包装机正常是指 X 应服从正态分布 N(0.5, 0.015²)。若 X 不是服从这个正态分布，则包装机就不正常了.

现在的问题是，如何根据样本观测值(9 袋味精的质量)来判断总体均值 μ 是否为 μ₀ = 0.5 kg(这里暂不考虑 σ 可能也改变的情形)。为此，我们提出假设 H₀ : μ = μ₀ = 0.5 称它为原假设或零假设.与这个假设相对应的假设是 H₁ : μ ≠ μ₀ 称它为备择假设.

于是问题转化为检验假设 H₀ 是否为真(成立).当 H₀ 为真,则认为机器正常.否则,认为机器不正常.

检验方法

我们的任务就是要根据样本对假设作出判断。

由于样本均值 $\bar{X} = \frac{1}{n}\sum_{i = 1}^n X_i$ 是总体均值 EX = μ 的无偏估计，故当 H₀ 为真时,X̄ 的观测值 x̄ 应落在 μ₀ 的附近，偏差 |x̄ − μ₀| 应很小.当 |x̄ − μ₀| 过分大时，我们就应当怀疑 H₀ 不正确而拒绝 H₀。但是如何给出一个明确的数量界限，以便确认偏差 |x̄ − μ₀| 是否过大的问题？

当 H₀ 为真时,$\bar{X} \sim N\left( \mu_0, \frac{\sigma^2}{n} \right)$,其中 μ₀, σ² 都是已知常数,所以统计量
$$ U = \frac{(\bar{X} - \mu_0)\sqrt{n}}{\sigma} \sim N(0, 1). $$ 给定实数 α(0 < α < 1),令 u_α 为标准正态分布上侧 α 分位数，则
$$ P\left( \left| \frac{(\bar{X} - \mu_0)\sqrt{n}}{\sigma} \right| > u_{\alpha/2} \right) = \alpha, \tag{8.1} $$

由于 α 通常是一个较小的数，所以事件
$$ \left\{ \left| \frac{(\bar{X} - \mu_0)\sqrt{n}}{\sigma} \right| > u_{\alpha/2} \right\} $$

是一个由样本 (X₁, X₂, ⋯, X_n) 构成的小概率事件，u_α/2 就是根据样本观测值确认小概率事件是否已发生的数量界限.

查 N(0, 1) 分布表可得 u_α/2 的值，将统计量 U 的观测值 $u = \frac{(\bar{x} - \mu_0)\sqrt{n}}{\sigma}$ 与 u_α/2 相比较，当 |u| > u_α/2 时，说明小概率事件在一次试验中发生了，这就与小概率事件在一次试验中不太可能发生的原理相矛盾，因而认为 H₀ 不真而拒绝 H₀；若 |u| ≤ u_α/2，则一次试验的结果与 H₀ 为真并无矛盾，因此没有理由拒绝 H₀，于是接受 H₀。

对于上面的例子，x̄ = 0.511,取 α = 0.05，查 N(0, 1) 分布表得 u_α/2 = u_0.025 = 1.96，又 n = 9,σ = 0.015,因而
$$ |u| = \left| \frac{(\bar{x} - \mu_0)\sqrt{n}}{\sigma} \right| = \left| \frac{0.511 - 0.5}{0.015} \sqrt{9} \right| = 2.2 > 1.96 = u_{\alpha/2}. $$ 小概率事件居然发生了，这与实际推断原理相矛盾，故拒绝 H₀，即认为 x̄ 与 μ₀ 已有了显著差异，从而抽取的 9 袋味精不是来自正态总体 N(0.5, 0.015²)，而是来自一个均值 μ ≠ 0.5 的正态总体。换句话说，这天包装机工作不正常。

构造小概率事件作用的统计量称为检验统计量。当统计量的观测值取某个区域 W 中的值时，我们拒绝 H₀，则称区域 W 为拒绝域，拒绝域的边界点称为临界点

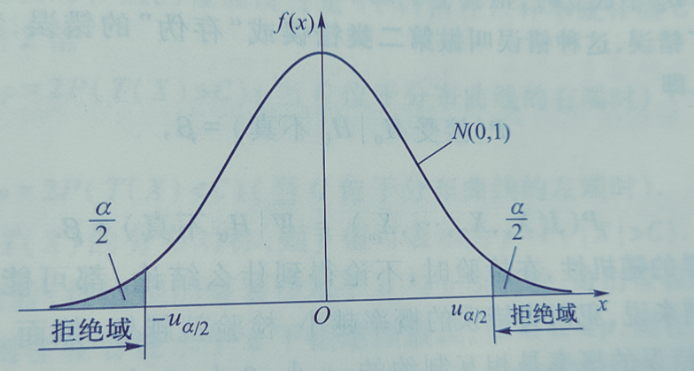
例如，在上面的例子中，检验统计量是 $\frac{(\bar{X} - \mu_0)\sqrt{n}}{\sigma}$，拒绝域 W = (−∞, −1.96) ∪ (1.96, +∞),−1.96 与 1.96 都是临界点

在检验中确立小概率事件的数 α，称为显著性水平或简称为水平，α 通常取 0.1,0.05 或 0.01。值得注意的是 α 取不同的值，检验结果可能不同，统计推断的可靠程度也不同。

例如,在例子中取 α = 0.01，则 u_α/2 = u_0.005 = 2.57，因此，|u| = 2.2 ≤ 2.57，依检验法则应接受 H₀。

检验是在假设 H₀ 与 H₁ 之间做选择，拒绝 H₀,意味着接受 H₁；接受 H₀,表示拒绝 H₁。所以,像例子这样一类的检验问题，通常称为在显著性水平 α 下的假设检验
H₀ : μ = μ₀; H₁ : μ ≠ μ₀,

简称为 H₀ 对 H₁ 的显著性检验.

总结一下：

我们希望通过样本数据判断总体参数（例如均值μ）是否属于某个假设，比如μ = μ₀

这就涉及到一个关键问题：样本均值$\overline X$和假设值μ₀的偏差$|\overline X - \mu_0|$多大才算“过分大”？需要给出一个明确的数学界限。

为什么用样本均值？
- 样本均值 $\overline X$ 是总体均值μ的无偏估计（即长期来看$\overline X = \mu$），所以如果H₀(μ = μ₀)为真， $\overline X$ 应该集中在 μ₀ 附近。
- 如果 $\overline X$ 离 μ₀ 太远，我们怀疑 H₀ 不成立。
如何量化“偏差是否过大”
- 直接比较 |X̄ − μ₀| 不够，因为数据波动大小（方差 σ²）和样本量 n 会影响结果。
- 解决方案：将偏差标准化，消除量纲和样本量影响，构造检验统计量： $$ U = \frac{(\bar{X} - \mu_0)\sqrt{n}}{\sigma} $$ 当 H₀ 为真时，U ∼ N(0, 1)（标准正态分布）。
如何确定拒绝界限？
- 选定显著性水平 α（如 0.05），表示容忍的误判概率（即 H₀ 为真但被拒绝的概率）。
- 查标准正态分布表，找到临界值 u_α/2（如 α = 0.05 时，u_0.025 = 1.96）。
- 拒绝域：如果 |U| > u_α/2，认为偏差“过大”，拒绝 H₀。

两类错误

在假设检验中，由于样本的随机性，我们可能会犯以下两类错误：

第一类错误（弃真错误）

定义：当原假设H₀实际上为真时，我们却拒绝了它。
表示： P(拒绝H₀|H₀为真) = α
特点：
- α是显著性水平，即检验中设定的阈值（通常取0.05, 0.01等）
- 好比”冤枉好人”的概率

第二类错误（存伪错误）

定义：当H₀实际上不成立时，我们却接受了它。
表示： P(接受H₀|H₀不成立) = β
特点：
- 相当于”放过坏人”的概率
- 计算β需要知道备择假设H₁的具体分布

两类错误的关系

此消彼长：当样本量n固定时，α减小会导致β增大，反之亦然
解决方案：增加样本量可以同时减小α和β

实际应用原则

原假设选择：
- 把希望验证的结论放在备择假设H₁
- 将历史结论或保守判断设为H₀
显著性水平选择：
- 医学等严格领域：取α = 0.01
- 一般社会科学：常用α = 0.05
检验效能：1 − β表示正确拒绝H₀的能力，好的检验应保证较高效能

错误类型	通俗比喻	概率表示	控制方法
第一类	冤枉好人	α	直接设定
第二类	放过坏人	β	增大样本量

简单总结一下

错误类型	概率	本例表现
第一类错误（弃真）	α	机器正常却判为异常
第二类错误（取伪）	β	机器异常却判为正常

假设检验的基本步骤

假设检验的本质是基于样本数据对总体参数做出概率性判断。其核心逻辑可分为三步：

设立对立假设：
- H₀ : μ = μ₀（原假设，默认成立）
- H₁ : μ ≠ μ₀（备择假设）
构造判断工具：
- 建立检验统计量 $U = \frac{(\bar{X} - \mu_0)\sqrt{n}}{\sigma}$
- 确定其分布 U ∼ N(0, 1)（当H₀为真时）
制定决策规则：
- 设定显著性水平 α（通常取0.05），确定拒绝域 W 的形式
- 计算临界值 u_α/2
- 比较统计量观测值|u|与临界值
根据统计量的观测值决定是拒绝还是接受H₀

如何确定拒绝域：

对于双侧检验拒绝域 = (−∞, −u_α/2) ∪ (u_α/2, +∞) 其中临界值u_α/2通过查表获得：

α = 0.05 ⇒ u_0.025 = 1.96
α = 0.01 ⇒ u_0.005 = 2.58

而基于小概率事件原理 P(|U| > u_α/2) = α 当α = 0.05时，意味着在H₀成立的假设下：

有95%的概率U会落在(−1.96, 1.96)之间
只有5%的概率会落入拒绝域

正态总体均值的假设检验

单个正态总体均值的检验

设总体 $ X $ 服从正态分布 $ N(, ^2) ， (X_1, X_2, , X_n) $ 为总体 $ X $ 的一个样本，欲检验假设：
H₀ : μ = μ₀; H₁ : μ ≠ μ₀ 其中 $ _0 $ 为已知常数.

根据总体方差 $ ^2 $ 是否已知，分为两种情形：

$ ^2$已知

结论

已求出统计量
$$ U = \frac{(\bar{X} - \mu_0)\sqrt{n}}{\sigma} $$ 在假设 $ H_0$ 成立时，服从 $ N(0, 1) $，拒绝域 $ W = (-, -u_{/2}) (u_{/2}, +) $

此检验法称为U检验法

推导过程

样本均值性质：由正态分布的性质可知，样本均值 $$ \bar{X} = \frac{1}{n}\sum_{i=1}^n X_i $$ 服从： $$ \bar{X} \sim N(\mu, \frac{\sigma^2}{n}) $$
标准化变换：当H₀成立时（μ = μ₀），构造统计量： $$ U = \frac{\bar{X} - \mu_0}{\sigma/\sqrt{n}} \sim N(0,1) $$
拒绝域确定：对于显著性水平α，查标准正态分布表得临界值u_α/2，使得： P(|U| ≥ u_α/2) = α 因此拒绝域为： W = {U ∣ U ≤ −u_α/2 或 U ≥ u_α/2}

实际计算示例

例题：已知某生产线灌装重量服从N(μ, 5²)，现抽取25瓶测得平均重量x̄ = 498g。检验平均重量是否为500g（α = 0.05）。

解题步骤：

建立假设： H₀ : μ = 500 vs H₁ : μ ≠ 500
计算检验统计量： $$ \begin{align*} U &= \frac{\bar{X} - \mu_0}{\sigma/\sqrt{n}} \\ &= \frac{498 - 500}{5/\sqrt{25}} \\ &= \frac{-2}{1} = -2.0 \end{align*} $$
确定临界值：查标准正态分布表得u_0.025 = 1.96
决策规则：
- 拒绝域：(−∞, −1.96] ∪ [1.96, +∞)
- 由于−2.0 < −1.96，落入拒绝域
结论：在α = 0.05水平下拒绝H₀，认为平均灌装重量与500g有显著差异。

$^2 $ 未知

结论

用 $ ^2 $ 的无偏估计 $ S^2 $ 去估计 $ ^2 $，则在假设 $ H_0 $ 成立时，统计量 $$ T = \frac{(\bar{X} - \mu_0)\sqrt{n}}{S} \sim t(n - 1) $$ 于是，对给定的水平 $ $，查 $ t $ 分布临界值表可得 $ t_{/2}(n - 1) ，使得$ P(|t| > t_{/2}(n - 1)) = 从而拒绝域为 W = (-, -t_{/2}(n - 1)) (t_{/2}(n - 1), +) $$ 此检验法称为t检验法

推导过程

样本方差替代：当总体方差σ²未知时，用样本方差 $$ S^2 = \frac{1}{n-1}\sum_{i=1}^n (X_i - \bar{X})^2 $$ 作为估计量。
统计量构造：

在H₀成立时（μ = μ₀），构造： $$ T = \frac{\bar{X} - \mu_0}{S/\sqrt{n}} $$
分布推导：
- 分子：$\bar{X} - \mu_0 \sim N(0, \frac{\sigma^2}{n})$
- 分母：$\frac{S}{\sqrt{n}}$是样本标准差的标准误
- 由统计学定理可知： $$ \frac{\bar{X} - \mu_0}{S/\sqrt{n}} \sim t(n-1) $$ 其中t(n − 1)表示自由度为n − 1的t分布
拒绝域确定：对于显著性水平α，查t分布表得临界值t_α/2(n − 1)，使得： P(|T| ≥ t_α/2(n − 1)) = α 因此拒绝域为： W = (−∞, −t_α/2(n − 1)] ∪ [t_α/2(n − 1), +∞)

实际计算示例

设某厂生产的螺杆直径服从正态分布 $ N(, ^2) ，现从中抽取5件，测得直径（单位：mm）为$ 22.3, 21.5, 22.0, 21.8, 21.4 $$ 若 $ ^2 $ 未知，试在显著性水平 $ = 0.05 $ 下，检验假设 $ H_0:= 21; H_1: $

由于方差 $ ^2 $ 未知，因此用 $ t $ 检验法.由样本观测值计算得 x̄ = 21.8, s² = 0.135

$$ t = \frac{21.8 - 21}{\sqrt{0.135 / 5}} = 4.87. $$

查 $ t $ 分布表得 $ t_{/2}(n - 1) = t_{0.025}(4) = 2.776 $.

由于 $ |t| = 4.87 > 2.776 = t_{/2}(n - 1) $，故拒绝 $ H_0 $，即在显著性水平 0.05 下认为螺杆直径不是 21 mm.

两个正态总体均值差的检验

设 X ∼ N(μ₁, σ₁²)，Y ∼ N(μ₂, σ₂²)，(X₁, X₂, ⋯, X_n₁) 和 (Y₁, Y₂, ⋯, Y_n₂) 分别是来自 X 和 Y 的样本且相互独立，考虑检验假设： H₀ : μ₁ − μ₂ = δ; H₁ : μ₁ − μ₂ ≠ δ 其中 δ 为已知常数，较常见的是 δ = 0，即检验两个正态总体的均值是否相等，取显著性水平为 α。下面分三种情况讨论。

$ _1^2$ 和 σ₂² 已知

结论

由于统计量 X̄ − Ȳ 是 μ₁ − μ₂ 的无偏估计量，因此在 H₀ 成立时，统计量 $$ U = \frac{\bar{X} - \bar{Y} - (\mu_1 - \mu_2)}{\sqrt{\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}}} \sim N(0, 1) $$ 于是，对给定的水平 α，查 N(0, 1) 分布临界值表可得 u_α/2，使得 P(|U| > u_α/2) = α 从而拒绝域为 W = (−∞, −u_α/2) ∪ (u_α/2, +∞) 由于检验统计量 U ∼ N(0, 1)，故此检验法仍为 U 检验法。

推导过程

样本均值性质：
- $\bar{X} \sim N\left(\mu_1, \frac{\sigma_1^2}{n_1}\right)$
- $\bar{Y} \sim N\left(\mu_2, \frac{\sigma_2^2}{n_2}\right)$
均值差分布：由独立性可知： $$ \bar{X} - \bar{Y} \sim N\left(\mu_1 - \mu_2, \frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}\right) $$
标准化变换：当H₀成立时（μ₁ − μ₂ = δ）： $$ U = \frac{(\bar{X} - \bar{Y}) - \delta}{\sqrt{\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}}} \sim N(0,1) $$
拒绝域确定：对于显著性水平α，查标准正态分布表得u_α/2，使得： P(|U| ≥ u_α/2) = α 因此拒绝域为： W = {U ∣ |U| ≥ u_α/2}

细节内容说明

协方差分析： Cov(X̄, Ȳ) = 0 (因样本独立)

方差分解： $$ \begin{align*} \text{Var}(\bar{X} - \bar{Y}) &= \text{Var}(\bar{X}) + \text{Var}(\bar{Y}) \\ &= \frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2} \end{align*} $$ **

正态线性组合性质：对于独立正态变量X ∼ N(μ_X, σ_X²)，Y ∼ N(μ_Y, σ_Y²)，有： aX + bY ∼ N(aμ_X + bμ_Y, a²σ_X² + b²σ_Y²) 此处取a = 1, b = −1即得X̄ − Ȳ的分布

实际计算示例

从甲、乙两厂生产的钢丝总体 X, Y 中各取 50 截 1 米长的钢丝作拉力强度试验，得 x̄ = 1208，ȳ = 1282。设钢丝的抗拉强度服从正态分布，且 σ_x² = 80²，σ_y² = 94²，问甲、乙两厂钢丝的抗拉强度是否有显著差别（α = 0.05）？

设甲、乙两厂钢丝抗拉强度总体均值分别为 μ_x 和 μ_y，考虑检验假设 H₀ : μ_x = μ_y; H₁ : μ_x ≠ μ_y 由题意知 n₁ = n₂ = 50，σ_x = 80，σ_y = 94，α = 0.05，查 N(0, 1) 分布表，得 u_α/2 = u_0.025 = 1.96。由于 $$ |u| = \left| \frac{\bar{x} - \bar{y}}{\sqrt{\frac{\sigma_x^2}{n_1} + \frac{\sigma_y^2}{n_2}}} \right| = \left| \frac{1208 - 1282}{\sqrt{\frac{80^2}{50} + \frac{94^2}{50}}} \right| = 4.24 > 1.96 $$ 故拒绝 H₀，即在显著性水平 0.05 下，认为两厂钢丝的抗拉强度有明显差别。

对这类检验问题，当拒绝原假设 H₀ 时，若想进一步知道是 μ_x > μ_y，还是 μ_x < μ_y，可作如下判断：若 U 的观测值 u > u_α/2，则认为 μ_x > μ_y；若 u < −u_α/2，则认为 μ_x < μ_y。

在例 8.3 中，u = −4.24 < −1.96 = −u_α/2，所以甲厂钢丝的抗拉强度明显低于乙厂

$ _1^2$ 和 σ₂² 都未知，但相等

结论

由于在 H₀ 成立时，统计量 $$ T = \frac{\bar{X} - \bar{Y} - (\mu_1 - \mu_2)}{\sqrt{\frac{(n_1 - 1)S_1^2 + (n_2 - 1)S_2^2}{n_1 + n_2 - 2}}} \cdot \sqrt{\frac{n_1 n_2(n_1 + n_2 - 2)}{n_1 + n_2}} \sim t(n_1 + n_2 - 2) $$

于是，对给定的水平 α，查 t 分布临界值表可得 t_α/2(n₁ + n₂ − 2)，使得

P(|T| > t_α/2(n₁ + n₂ − 2)) = α

从而拒绝域为 W = (−∞, −t_α/2(n₁ + n₂ − 2)) ∪ (t_α/2(n₁ + n₂ − 2), +∞) 由于检验统计量 T ∼ t(n₁ + n₂ − 2)，故此检验法也称 t 检验法

推导过程

合并方差估计：构造合并样本方差（Pooled Variance）： $$ S_p^2 = \frac{(n_1-1)S_1^2 + (n_2-1)S_2^2}{n_1+n_2-2} $$ 其中S₁²和S₂²分别为两样本的样本方差
统计量构造：在H₀成立时（μ₁ − μ₂ = δ）： $$ T = \frac{(\bar{X} - \bar{Y}) - \delta}{S_p\sqrt{\frac{1}{n_1} + \frac{1}{n_2}}} $$
分布推导：
- 分子：$\bar{X} - \bar{Y} \sim N\left(0, \sigma^2\left(\frac{1}{n_1} + \frac{1}{n_2}\right)\right)$
- 分母：$\sqrt{\frac{S_p^2}{\sigma^2}} \sim \sqrt{\frac{\chi^2(n_1+n_2-2)}{n_1+n_2-2}}$
- 由t分布定义可得： T ∼ t(n₁ + n₂ − 2)
简化形式：统计量可表示为： $$ T = \frac{\bar{X} - \bar{Y} - \delta}{\sqrt{\frac{(n_1-1)S_1^2 + (n_2-1)S_2^2}{n_1+n_2-2}} \cdot \sqrt{\frac{n_1n_2}{n_1+n_2}}} $$

细节说明

方差齐性假设： σ₁² = σ₂² = σ²

合并方差的无偏性： E(S_p²) = σ²

独立性的运用：

X̄与S₁²独立，Ȳ与S₂²独立

两样本相互独立

t分布的形成： $$ \frac{N(0,1)}{\sqrt{\chi^2(k)/k}} \sim t(k) $$ 此处k = n₁ + n₂ − 2

实际计算示例

在漂白工艺中考查温度对针织品断裂强度的影响，今在 70^∘C 和 80^∘C 分别作 8 次和 6 次试验，测得各自的断裂强度 X 和 Y 的观测值。经计算得 x̄ = 20.4，ȳ = 19.3167，s₁² = 0.886，s₂² = 1.0566，根据以往的经验，可以认为 X 和 Y 均服从正态分布，且方差相等，在给定 α = 0.10 时，问 70^∘C 与 80^∘C 对断裂强度有无显著差异？

由题设，可假定 X ∼ N(μ₁, σ²)，Y ∼ N(μ₂, σ²)，考虑检验假设

取上式定义的检验统计量 T，由 α = 0.10，查 t 分布表，得 t_α/2(n₁ + n₂ − 2) = t_0.05(12) = 1.782。由于 T 的观测值 $$ |t| = \frac{|\bar{x} - \bar{y}|}{\sqrt{\frac{(n_1 - 1)s_1^2 + (n_2 - 1)s_2^2}{n_1 + n_2 - 2}}} \cdot \sqrt{\frac{n_1 n_2(n_1 + n_2 - 2)}{n_1 + n_2}} = 2.0504 > 1.782 $$ 即 t ∈ W，故拒绝 H₀。换言之，在显著性水平 0.10 下，认为 70^∘C 与 80^∘C 的断裂强度有明显差异。

σ₁² ≠ σ₂² 且都未知，但n₁ = n₂ = n（配对问题）

结论

考虑检验假设 H₀ : μ₁ = μ₂; H₁ : μ₁ ≠ μ₂ 令 Z_i = X_i − Y_i, i = 1, 2, ⋯, n 记 $$ EZ_i = E(X_i - Y_i) = \mu_1 - \mu_2 = d \\ D(Z_i) = D(X_i - Y_i) = DX_i + DY_i = \sigma_1^2 + \sigma_2^2 = \sigma^2 $$ 则 (Z₁, Z₂, ⋯, Z_n) 是正态总体 Z ∼ N(d, σ²) 的样本。于是检验假设（8.8）就等价于检验假设： H₀ : d = 0; H₁ : d ≠ 0 于是用 t 检验法，在 H₀ 成立时，统计量 $$ T = \frac{\bar{Z}}{S} \sqrt{n} \sim t(n - 1) $$ 其中 $\bar{Z} = \frac{1}{n}\sum_{i = 1}^n Z_i$，$S^2 = \frac{1}{n - 1}\sum_{i = 1}^n (Z_i - \bar{Z})^2$，其拒绝域为 W = (−∞, −t_α/2(n − 1)) ∪ (t_α/2(n − 1), +∞)

详细推导

配对差值的构造：定义配对差值： Z_i = X_i − Y_i, i = 1, 2, ..., n 由正态分布的性质： Z_i ∼ N(d, σ²) 其中： d = μ₁ − μ₂, σ² = σ₁² + σ₂²
样本均值与方差：
- 样本均值： $$ \bar{Z} = \frac{1}{n}\sum_{i=1}^n Z_i \sim N\left(d, \frac{\sigma^2}{n}\right) $$
- 样本方差： $$ S^2 = \frac{1}{n-1}\sum_{i=1}^n (Z_i - \bar{Z})^2 $$
检验统计量的构建：当H₀成立时（d = 0）： $$ T = \frac{\bar{Z} - 0}{S/\sqrt{n}} = \frac{\bar{Z}}{S}\sqrt{n} $$
分布推导：
- 分子标准化： $$ \frac{\bar{Z}}{\sigma/\sqrt{n}} \sim N(0,1) $$
- 分母调整： $$ \frac{(n-1)S^2}{\sigma^2} \sim \chi^2(n-1) $$
- 由t分布定义： $$ T = \frac{N(0,1)}{\sqrt{\chi^2(n-1)/(n-1)}} \sim t(n-1) $$
拒绝域确定：对于显著性水平α，查t分布表得临界值t_α/2(n − 1)，拒绝域为： |T| > t_α/2(n − 1)

实际问题示例

为比较甲、乙两种橡胶轮胎的耐磨性，从两种轮胎中各随机地抽取 8 个，又各取一个组成一对，再随机地选取 8 架飞机，将 8 对轮胎随机地分配给 8 架飞机作耐磨试验，经飞行起落一段时间后，测得轮胎磨损量（单位：mg）数据如下：

甲	4900	5220	5500	6020	6340	7660	8650	4870
乙	4930	4900	5140	5700	6110	6880	7930	5010

设轮胎磨损量都服从正态分布，问这两种轮胎的耐磨性有无显著差别（$ = 0.05 $）.

因是配对数据，令 $ Z = X - Y $，则由题意得 $ Z $ 的 8 个观测数据为： −30, 320, 360, 320, 230, 780, 720, − 140 则原检验问题化为： H₀ : d = 0; H₁ : d ≠ 0 经计算求得 $ {z} = 320 ， s^2 = 102200 $。取定义统计量 $ T $，由 $ = 0.05 $，查 $ t $ 分布表，得 $ t_{/2}(n - 1) = t_{0.025}(7) = 2.365 $。由于 $ T $ 的观测值 $$ |t| = \left| \frac{\bar{z}}{s} \sqrt{8} \right| \approx 2.83 > 2.365 $$ 故拒绝 $ H_0 $，即在显著性水平 0.05 下，认为两种轮胎的耐磨性有显著的差异

正态总体方差的假设检验

单个正态总体方差的检验

设总体X服从正态分布N(μ, σ²)，(X₁, X₂, ⋯, X_n)为总体X的一个样本，欲检验假设： H₀ : σ² = σ₀²; H₁ : σ² ≠ σ₀² 其中σ₀²为已知常数。

μ已知的情形

结论

构造统计量： $$ \chi^2 = \frac{\sum_{i=1}^n (X_i - \mu)^2}{\sigma_0^2} $$ 在假设H₀成立时，服从χ²(n)分布，拒绝域为： W = (0, χ_{1 − α/2}²(n)) ∪ (χ_α/2²(n), +∞)

推导过程

样本性质：由于X_i ∼ N(μ, σ²)，有： $$ \frac{X_i - \mu}{\sigma_0} \sim N(0,1) $$
卡方统计量构造：由卡方分布定义： $$ \sum_{i=1}^n \left(\frac{X_i - \mu}{\sigma_0}\right)^2 \sim \chi^2(n) $$
拒绝域确定：对于显著性水平α，查卡方分布表得临界值χ_α/2²(n)和χ_{1 − α/2}²(n)，使得： $$ P(\chi^2 \leq \chi^2_{1-\alpha/2}(n)) = \frac{\alpha}{2} \\ P(\chi^2 \geq \chi^2_{\alpha/2}(n)) = \frac{\alpha}{2} $$

μ未知的情形

结论

构造统计量： $$ \chi^2 = \frac{(n-1)S^2}{\sigma_0^2} $$ 在假设H₀成立时，服从χ²(n − 1)分布，拒绝域为： W = (0, χ_{1 − α/2}²(n − 1)) ∪ (χ_α/2²(n − 1), +∞)

推导过程

样本方差性质：样本方差： $$ S^2 = \frac{1}{n-1}\sum_{i=1}^n (X_i - \bar{X})^2 $$
卡方统计量构造：由统计学定理： $$ \frac{(n-1)S^2}{\sigma_0^2} \sim \chi^2(n-1) $$
拒绝域确定：对于显著性水平α，查卡方分布表得临界值χ_α/2²(n − 1)和χ_{1 − α/2}²(n − 1)。

实际计算示例

例题：某机器生产的零件长度服从N(μ, σ²)，现抽取16个零件测得样本方差s² = 0.025。检验总体方差是否为0.02（α = 0.05）。

解题步骤：

建立假设： H₀ : σ² = 0.02 vs H₁ : σ² ≠ 0.02
计算检验统计量： $$ \chi^2 = \frac{(n-1)s^2}{\sigma_0^2} = \frac{15 \times 0.025}{0.02} = 18.75 $$
确定临界值：查卡方分布表得χ_0.025²(15) = 27.488，χ_0.975²(15) = 6.262
决策规则：
- 拒绝域：(0, 6.262] ∪ [27.488, +∞)
- 由于6.262 < 18.75 < 27.488，未落入拒绝域
结论：在α = 0.05水平下不能拒绝H₀，认为总体方差与0.02无显著差异。

假设检验

什么是参数的假设检验

检验方法

两类错误

第一类错误（弃真错误）

第二类错误（存伪错误）

两类错误的关系

实际应用原则

假设检验的基本步骤

正态总体均值的假设检验

单个正态总体均值的检验

$ ^2$已知

结论

推导过程

实际计算示例

$^2 $ 未知

结论

推导过程

实际计算示例

两个正态总体均值差的检验

$ _1^2$ 和 σ22 已知

结论

推导过程

实际计算示例

$ _1^2$ 和 σ22 都未知，但相等

结论

推导过程

实际计算示例

σ12 ≠ σ22 且都未知，但n1 = n2 = n（配对问题）

结论

详细推导

实际问题示例

正态总体方差的假设检验

单个正态总体方差的检验

μ已知的情形

结论

推导过程

μ未知的情形

结论

推导过程

实际计算示例

两个正态总体的情况

$ _1^2$ 和 σ₂² 已知

$ _1^2$ 和 σ₂² 都未知，但相等

σ₁² ≠ σ₂² 且都未知，但n₁ = n₂ = n（配对问题）