问题

一个容量为 m 公斤的背包，现在有 n 种物品，每种物品只有一件，每件物品有其自身的重量 weight[i] 和价值 value[i]。

选择哪些物品装入背包，使得在不超过背包总承重的前提下，装入背包的物品总价值最大。

image-20251115191200115

思路

这就是著名的0-1背包问题。“0-1”意味着每种物品只有一件，你只能选择装入（1）或不装入（0），不能只装入部分。

要解决 01 背包问题，我们可以使用动态规划的方法。核心思路是通过一个二维数组 dp 来记录状态，其中 dp[i][j] 表示前 i 件物品在背包容量为 j 时能获得的最大价值。

那么每种物品只有一件，选择时只有 “放入背包” 或 “不放入背包” 两种状态。

所以我们需要在背包容量限制下，选择物品使得总价值最大。

动态规划通过填表的方式，记录并利用已解决的子问题的答案，从而避免重复计算，极大地提高效率

考虑动态规划，就这三步

  • 确定状态变量（函数）
  • 确定状态的转移方程（递推关系）
  • 确定边界条件

那么我们可以这样考虑动态规划

  1. 状态定义：dp[i][j] 表示前 i 件物品，背包容量为 j 时的最大价值。

  2. 状态转移：

    • 如果不放入第 i 件物品：dp[i][j] = dp[i-1][j]（价值与前 i-1 件物品在容量 j 时的最大价值相同）。
    • 如果放入第 i 件物品（需满足 j >= w[i]）：dp[i][j] = dp[i-1][j - w[i]] + c[i]（前 i-1 件物品在容量 j - w[i] 时的最大价值，加上第 i 件物品的价值）。
    • 最终 dp[i][j] 取两种情况的最大值：dp[i][j] = max(dp[i-1][j], dp[i-1][j - w[i]] + c[i])（当 j >= w[i] 时）。
    image-20251115192057305

  3. 初始状态：dp[0][j] = 0（前 0 物品，价值为 0）；dp[i][0] = 0（背包容量为 0，价值为 0），所有物品一开始都没有放入背包，所以 f[i][j] = 0

image-20251115191518387

注意，把 dp[i][j] 中的 i，需要考虑成物品的范围。dp[0][j]表示一件物品都不考虑。

模板代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();  // 物品数量
        int m = sc.nextInt();  // 背包容量
        int[] w = new int[n + 1];  // 物品重量，w[0]无用
        int[] c = new int[n + 1];  // 物品价值，c[0]无用
        for (int i = 1; i <= n; i++) {
            w[i] = sc.nextInt();
            c[i] = sc.nextInt();
        }

        // dp[i][j]：前i件物品，背包容量j时的最大价值
        int[][] dp = new int[n + 1][m + 1];

        // 动态规划填表
        for (int i = 1; i <= n; i++) { // 遍历每件物品
            for (int j = 1; j <= m; j++) { // 遍历背包容量
                if (j < w[i]) {
                    // 背包容量不足，无法放入第i件物品
                    dp[i][j] = dp[i - 1][j];
                } else {
                    // 可以选择放入或不放入，取最大值
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - w[i]] + c[i]);
                }
            }
        }

        System.out.println(dp[n][m]); // 前n件物品，背包容量m时的最大价值
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include <iostream>
#include <algorithm>
using namespace std;

int main() {
    int n, m;
    cin >> n >> m;  // 物品数量和背包容量
    
    int* w = new int[n + 1];  // 物品重量，w[0]无用
    int* c = new int[n + 1];  // 物品价值，c[0]无用
    
    for (int i = 1; i <= n; i++) {
        cin >> w[i] >> c[i];
    }
    
    // dp[i][j]：前i件物品，背包容量j时的最大价值
    int** dp = new int*[n + 1];
    for (int i = 0; i <= n; i++) {
        dp[i] = new int[m + 1]();  // 初始化数组元素为0
    }
    
    // 动态规划填表
    for (int i = 1; i <= n; i++) {  // 遍历每件物品
        for (int j = 1; j <= m; j++) {  // 遍历背包容量
            if (j < w[i]) {
                // 背包容量不足，无法放入第i件物品
                dp[i][j] = dp[i - 1][j];
            } else {
                // 可以选择放入或不放入，取最大值
                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + c[i]);
            }
        }
    }
    
    cout << dp[n][m] << endl;  // 前n件物品，背包容量m时的最大价值
    
    // 释放动态分配的内存
    for (int i = 0; i <= n; i++) {
        delete[] dp[i];
    }
    delete[] dp;
    delete[] w;
    delete[] c;
    
    return 0;
}

样例分析

样例输入：

1
2
3
4
3 6
3 5
2 3
4 6
  • 物品 1：重量 3，价值 5；物品 2：重量 2，价值 3；物品 3：重量 4，价值 6；背包容量 6。

我们逐步推导 dp 数组：

  • 当i=1（处理物品 1）：
    • 当容量 j<3 时，dp[1][j] = 0；
    • 当容量 j>=3 时，dp[1][j] = 5（放入物品 1）。
  • 当i=2（处理物品 2）：
    • 当容量 j<2 时，dp[2][j] = dp[1][j]；
    • 当容量 2<=j<3 时，dp[2][j] = max(dp[1][j], dp[1][j-2]+3) = max(0, 3) = 3；
    • 当容量 3<=j<5 时，dp[2][j] = max(5, dp[1][j-2]+3)（如 j=3 时，max(5, 0+3)=5；j=4 时，max(5, 5+3)=8）；
    • 当容量 j>=5 时，dp[2][j] = max(5, 5+3)=8。
  • 当i=3（处理物品 3）：
    • 当容量 j<4 时，dp[3][j] = dp[2][j]；
    • 当容量4<=j<=6时，dp[3][j] = max(dp[2][j], dp[2][j-4]+6)
      • 例如 j=6 时：dp[2][6]=8，dp[2][6-4]+6 = dp[2][2]+6 = 3+6=9，所以 dp[3][6]=9（即样例输出）。

这种方法的时间复杂度是 O(n*m)（n 是物品数，m 是背包容量），空间复杂度也是 O(n*m)，对于题目给定的约束（n<51，m<201）完全适用。

滚动数组优化空间

优化思路

01 背包是好啊，但是情况来了，它需要 O(n*m)的空间，这对空间不友好的Java语言很容易MLE，怎么办

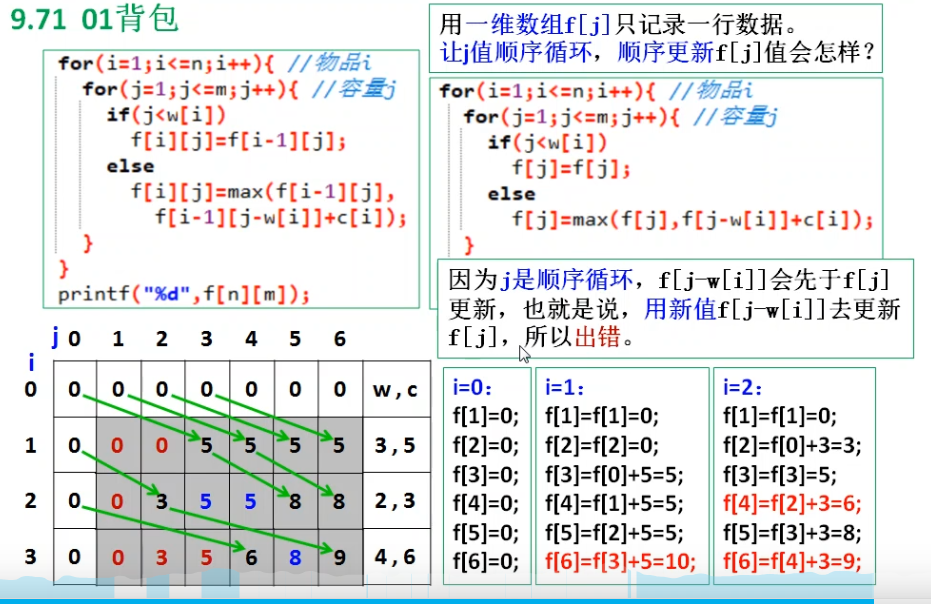
如果我们用一维的数组 f[j] 只记录一行数据，让 j值顺序循环，顺序更新f[j] 值会怎么样

这就是滚动数组优化

二维 dp 数组中，dp[i][j] 只依赖上一行 dp[i-1][...] 的数据来更新，要么取dp[i-1][j]，要么取dp[i-1][j-wei[i]]。

这意味着我们不需要保存所有行的历史数据，只需要用一个一维数组滚动覆盖，就能复用空间。

如果用一维数组 dp[j]（表示容量 j 时的最大价值），直接顺序枚举 j 会出问题：

  • 顺序枚举（j 从 wei [i] 到m）时，dp[j-wei[i]] 会先被当前物品 i 的更新覆盖（变成dp[i][j-wei[i]]）。
  • 而 01 背包要求每件物品只能用一次，必须依赖上一轮（i-1）未被覆盖的旧值 dp[i-1][j-wei[i]]。
image-20251115193258724

所以很明显，需要逆序枚举（j 从 m 到 wei [i]）能解决这个问题：

  • 从大到小遍历容量，dp[j-wei[i]] 还没被当前物品 i 更新，保留的是上一轮（i-1）的旧值。
  • 这样 dp[j] = max(dp[j], dp[j-wei[i]] + val[i]) 就和二维数组的转移逻辑完全一致。
二维数组逻辑 一维滚动数组逻辑
dp[i][j] = dp[i-1][j] 不做操作（一维数组保留上轮旧值）
dp[i][j] = max(dp[i-1][j], dp[i-1][j-wei[i]] + val[i]) dp[j] = max(dp[j], dp[j-wei[i]] + val[i])（逆序枚举 j）

优化后

  • 初始化：一维dp[0...m] 初始为 0，因为不放入物品，和二维数组dp[0][j] = 0、dp[i][0] = 0 一致。
  • 物品遍历：外层循环从 1 到 n，逐个处理每件物品。
  • 容量遍历：内层循环从 m 逆序到 wei [i]，只处理能装下当前物品的容量。
  • 状态转移方程：
    • 装不下（j < w[i]）：f[j] = f[j]，不装
    • 装得下，取大的：f[j] = max(f[j],f[j]-w[i]] + c[i])

模板代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int m = sc.nextInt();
        int[] val = new int[n + 1];
        int[] wei = new int[n + 1];
        // 滚动数组优化掉一维，逆序枚举
        int[] dp = new int[m + 1];

        for (int i = 1; i <= n; i++) {
            wei[i] = sc.nextInt();
            val[i] = sc.nextInt();
        }

        for(int i = 1; i <= n; i++){
            // 用旧值f[j-w[i]]更新f[j]，相当于用上一行的取更新,所以是逆序
            // 背包容量逆序循环，避免顺序循环时候f[j-w[i]]先于f[j]更新
            for(int j = m; j >= wei[i]; j--){
                //if(j < wei[i]){
                //dp[j] = dp[j];
                //}else{
                dp[j] = Math.max(dp[j], dp[j - wei[i]] + val[i]);
            }
        }

        System.out.println(dp[m]);

        sc.close();
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

int main() {
    int n, m;
    cin >> n >> m;
    
    vector<int> val(n + 1);
    vector<int> wei(n + 1);
    vector<int> dp(m + 1, 0);  // 滚动数组，初始化为0
    
    // 读取物品的重量和价值
    for (int i = 1; i <= n; ++i) {
        cin >> wei[i] >> val[i];
    }
    
    // 0-1背包核心逻辑，逆序遍历避免重复使用物品
    for (int i = 1; i <= n; ++i) {
        for (int j = m; j >= wei[i]; --j) {
            dp[j] = max(dp[j], dp[j - wei[i]] + val[i]);
        }
    }
    
    cout << dp[m] << endl;
    
    return 0;
}

例题

P2430 严酷的训练

题目背景

Lj 的朋友 WKY 是一名神奇的少年，在同龄人之中有着极高的地位。。。

题目描述

他的老师老王对他的程序水平赞叹不已，于是下决心培养这名小子。

老王的训练方式很奇怪，他会一口气让 WKY 做很多道题，要求他在规定的时间完成。而老王为了让自己的威信提高，自己也会把这些题都做一遍。

WKY 和老王都有一个水平值，他们水平值的比值和做这些题所用时间的比值成反比。比如如果 WKY 的水平值是 1，老王的水平值是 2，那么 WKY 做同一道题的时间就是老王的 2 倍。

每个题目有他所属的知识点，这我们都知道，比如递归，动规，最短路，网络流。在这里我们不考虑这些事情，我们只知道他们分别是知识点 1，知识点 2……每一个知识点有他对应的难度，比如动态规划经常难于模拟。

而每一个同一知识点下的题目，对于 WKY 来讲，都是一样难的。而做出每一道题，老王都有其独特的奖励值。而奖励值和题目的知识点没有必然联系。

现在 WKY 同学请你帮忙，计算在老王规定的时间内，WKY 所能得到最大奖励值是多少 。

输入格式

输入文件包括以下内容：

第一行：

WKY 的水平值和老王的水平值。

数据保证 WKY 的水平值小于老王的水平值（哪怕它不现实），且老王的水平值是 WKY 的水平值的整数倍。

第二行：

题目的总数 m 和知识点的总数 n。

第三行：

n 个整数。第 i 个整数表示老王在做第 i 个知识点的题目所需的时间。

接下来有 m 行数每一行包括两个整数 p，q 。p 表示该题目所属的知识点，q 表示该题目对应的奖励值。

最后一行是规定的时间。

输出格式

输出文件只有一行，表示能到得到的最大奖励值。

输入输出样例 #1

输入 #1

1
2
3
4
5
6
7
8
9
10
1 2
6 4
1 2 3 4
1 5
2 6
3 3
4 8
3 3
4 5
20

输出 #1

1
22

说明/提示

对于 100% 的数据，1 ≤ n, m ≤ 100，规定时间  ≤ 5000。1 ≤ p ≤ n，1 ≤ q ≤ 1000。

看得出来，这道题是典型的01 背包问题，核心思路是先计算出每个题目对 WKY 的耗时，再通过 01 背包算法在规定时间内选择题目以获得最大奖励值。

WKY 与老王的水平值比值，和他们做同一题的时间比值成反比。

  • 设 WKY 的水平值为a，老王的为b（题目说明b是a的整数倍，且a < b）。
  • 则：WKY的时间 / 老王的时间 = b / a → WKY 的时间 = 老王的时间 × (b/a)。

那么

  • 背包容量：规定的总时间。
  • 物品：每个题目，重量 = WKY 解决每个知识点的耗时，价值 = 题目奖励值。
  • 问题转化为：从m个物品中选择，总重量不超过背包容量，总价值最大。

就可以知道转移方程是：f[j] = max(f[j], f[j − t[p[i]]] + q[i])

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);

        // 读取WKY和老王的水平值
        int a = sc.nextInt();
        int b = sc.nextInt();

        // 读取题目总数和知识点总数
        int m = sc.nextInt();
        int n = sc.nextInt();

        // 存储每个题目的知识点和奖励值
        int[] p = new int[m + 1];  // 知识点
        int[] q = new int[m + 1];  // 奖励值

        // 存储老王和WKY做各知识点题目的时间
        int[] t_lw = new int[n + 1];  // 老王的时间
        int[] t_wky = new int[n + 1];  // WKY的时间（计算得出）
        int ratio = b / a;  // 时间比例系数

        for (int i = 1; i <= n; i++) {
            t_lw[i] = sc.nextInt();
            t_wky[i] = t_lw[i] * ratio;  // 计算WKY的耗时
        }

        for (int i = 1; i <= m; i++) {
            p[i] = sc.nextInt();
            q[i] = sc.nextInt();
        }

        // 读取规定的总时间
        int t = sc.nextInt();

        // dp数组：dp[j]表示时间不超过j时的最大奖励值
        int[] dp = new int[t + 1];

        // 01背包核心逻辑
        for(int i = 1; i <= m; i++){
            // 逆序遍历时间，避免重复选择同一题目
            for(int j = t; j >= t_wky[p[i]]; j--){
                dp[j] = Math.max(dp[j], dp[j - t_wky[p[i]]] + q[i]);
            }
        }

        // 输出最大奖励值
        System.out.println(dp[t]);

        sc.close();
    }
}
image-20251115200913000