问题

继续 LCS 的问题考虑（本来是一篇文章，我感觉拆开好点）

问题又出现变化了，现在如果，我们要求求最长公共子串，也就是在 LCS 的基础上，要求连续

最长公共字串（LCStr）就是两个序列中连续且相同的最长子序列（区别于 LCS 的 “不要求连续”）

  • 序列 A："ABCBDAB"
  • 序列 B："BDCAB"
对比维度 最长公共子序列（LCS） 最长公共字串（LCStr）
核心要求 元素相对顺序一致，不要求连续 元素连续且相对顺序一致
示例结果 "BCAB"（长度 4） "AB" 或 "BD"（长度 2）
问题本质 找 “有序不连续” 的最长交集 找 “有序且连续” 的最长交集

那么问题就被定义为，给定两个字符串 S（长度 n）和 T（长度 m），找到它们之间长度最长的公共连续子串，输出其长度（若不存在则输出 0）。

image-20251116195531260

问题分析

根据 LCS 的基础，我们考虑动态规划

首先考虑状态定义

设 S 长度为 n，T 长度为 m，定义二维 DP 数组dp[i][j]：

  • 表示以 S 的第 i 个字符（S [i-1]，因数组索引从 0 开始）和 T 的第 j 个字符（T [j-1]）为结尾的最长公共字串长度。

可以看到和 LCS 不一样， LCStr 要求数组是代表以当前字符为结尾

为什么要 “以当前字符为结尾”？

因为字串要求连续，如果 S [i-1] 和 T [j-1] 相同，那么公共字串只能是 “以 S [i-2] 和 T [j-2] 为结尾的公共字串” 后面追加当前字符；如果不同，当前位置不可能构成公共字串，长度直接为 0。

所以说，只有当两字符串中的字符连续且相等的时候，公共子串的长度才能不断增加，否则就清零

image-20251116195759382

那么就可以考虑推导状态转移方程了

基于 “连续” 的核心要求，转移逻辑非常清晰：

  1. 当S[i-1] == T[j-1]（当前字符相同）：
    • 以 S [i-1]和 T [j-1] 为结尾的公共字串，是 “以 S [i-2]和 T [j-2]为结尾的公共字串” 的延长；
    • 因此dp[i][j] = dp[i-1][j-1] + 1（若 i=0 或 j=0，说明是第一个字符匹配，dp[i][j] = 1）。
  2. 当S[i-1] != T[j-1]（当前字符不同）：
    • 以这两个字符为结尾的公共字串不存在（因为连续中断）；
    • 因此dp[i][j] = 0（这是和 LCS 最核心的区别：LCS 此处取 max (dp [i-1][j], dp [i][j-1])，而字串因连续要求直接置 0）。

考虑初始状态

  • 当 i=0（S 为空串）：dp[0][j] = 0（空串和任何字符串的公共字串长度为 0）；
  • 当 j=0（T 为空串）：dp[i][0] = 0（同理）

时空复杂度分析

  • 时间复杂度：O (n×m)。需遍历 DP 数组的所有 (n+1)×(m+1) 个元素（实际是 n×m 次有效计算），每次计算仅需 O (1)；
  • 空间复杂度：O (n×m)。因使用了二维 DP 数组存储状态。

模板代码

Java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
import java.util.Scanner;

public class LongestCommonSubstring {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        String S = scanner.nextLine();
        String T = scanner.nextLine();
        scanner.close();

        int n = S.length();
        int m = T.length();
        // 初始化DP数组：(n+1)行(m+1)列，默认全0
        int[][] dp = new int[n + 1][m + 1];
        int maxLen = 0; // 记录最长公共字串长度

        // 遍历所有字符组合
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                if (S.charAt(i - 1) == T.charAt(j - 1)) {
                    // 字符匹配，长度=上一轮左上角+1
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                    // 更新最大长度
                    if (dp[i][j] > maxLen) {
                        maxLen = dp[i][j];
                    }
                } else {
                    // 字符不匹配，长度置0
                    dp[i][j] = 0;
                }
            }
        }

        System.out.println("最长公共字串长度：" + maxLen);
    }
}

C++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <iostream>
#include <string>
#include <vector>
using namespace std;

int main() {
    string S, T;
    getline(cin, S);  // 读取第一个字符串
    getline(cin, T);  // 读取第二个字符串
    
    int n = S.size();
    int m = T.size();
    // 初始化DP数组：(n+1)行(m+1)列，默认全0
    vector<vector<int>> dp(n + 1, vector<int>(m + 1, 0));
    int maxLen = 0;  // 记录最长公共字串长度
    
    // 遍历所有字符组合
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= m; ++j) {
            if (S[i - 1] == T[j - 1]) {
                // 字符匹配，长度=上一轮左上角+1
                dp[i][j] = dp[i - 1][j - 1] + 1;
                // 更新最大长度
                if (dp[i][j] > maxLen) {
                    maxLen = dp[i][j];
                }
            } else {
                // 字符不匹配，长度置0（vector初始化已为0，可省略）
                dp[i][j] = 0;
            }
        }
    }
    
    cout << "最长公共字串长度：" << maxLen << endl;
    return 0;
}

Python

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
S = input().strip()
T = input().strip()

n = len(S)
m = len(T)
# 初始化DP数组：(n+1)行(m+1)列，默认全0
dp = [[0] * (m + 1) for _ in range(n + 1)]
max_len = 0  # 记录最长公共字串长度

# 遍历所有字符组合
for i in range(1, n + 1):
    for j in range(1, m + 1):
        if S[i - 1] == T[j - 1]:
            # 字符匹配，长度=上一轮左上角+1
            dp[i][j] = dp[i - 1][j - 1] + 1
            # 更新最大长度
            if dp[i][j] > max_len:
                max_len = dp[i][j]
        else:
            # 字符不匹配，长度置0（列表初始化已为0，可省略）
            dp[i][j] = 0

print(f"最长公共字串长度：{max_len}")

考虑优化

优化思路

观察状态转移方程：dp[i][j]只依赖于dp[i-1][j-1]（上一行左上角的元素），而不依赖于同一行或同一列的其他元素。

那么，存鸡毛啊，仅需一个变量记录 “上一个状态的值” 不就可以了？

用一个变量prev存储dp[i-1][j-1]（即上一轮左上角的值）

再用一个变量maxLen实时记录当前找到的最长公共字串长度；

遍历 S 和 T 的每个字符（i 从 0 到 n-1，j 从 0 到 m-1）：

  1. 若 S [i] == T [j]：
    • 若 i=0 或 j=0（第一个字符匹配），当前长度curr = 1；
    • 否则curr = prev + 1；
    • 更新maxLen = max(maxLen, curr)；
  2. 若 S [i] != T [j]：
    • 当前长度curr = 0；
  3. 关键：将prev更新为curr（为下一轮 j+1 的计算准备，因为下一轮 j+1 的 “左上角” 就是当前 j 的curr）；
  4. 注意：每轮 j 遍历结束后，需重置prev = 0（避免跨行影响）。

考虑优化后复杂度

  • 时间复杂度：仍 O (n×m)（遍历次数不变）；
  • 空间复杂度：O (1)（仅用 2 个变量存储状态和最大长度）。

优化代码

Java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
import java.util.Scanner;

public class LongestCommonSubstringOpt {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        String S = scanner.nextLine();
        String T = scanner.nextLine();
        scanner.close();

        int n = S.length();
        int m = T.length();
        int maxLen = 0;
        int prev = 0; // 存储dp[i-1][j-1]的值

        for (int i = 0; i < n; i++) {
            prev = 0; // 每一行开始前重置prev（避免跨列影响）
            for (int j = 0; j < m; j++) {
                int curr;
                if (S.charAt(i) == T.charAt(j)) {
                    if (i == 0 || j == 0) {
                        curr = 1; // 第一个字符匹配，长度1
                    } else {
                        curr = prev + 1; // 继承上一轮左上角的值
                    }
                    maxLen = Math.max(maxLen, curr);
                } else {
                    curr = 0; // 不匹配，长度0
                }
                prev = curr; // 更新prev，为下一个j+1做准备
            }
        }

        System.out.println("最长公共字串长度：" + maxLen);
    }
}

C++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include <iostream>
#include <string>
#include <algorithm>
using namespace std;

int main() {
    string S, T;
    getline(cin, S);  // 读取第一个字符串
    getline(cin, T);  // 读取第二个字符串
    
    int n = S.size();
    int m = T.size();
    int maxLen = 0;
    int prev = 0;  // 存储上一轮的dp[i-1][j-1]值
    
    for (int i = 0; i < n; ++i) {
        prev = 0;  // 每行开始前重置prev
        for (int j = 0; j < m; ++j) {
            int curr;
            if (S[i] == T[j]) {
                // 边界情况：第一行或第一列，匹配则长度为1
                if (i == 0 || j == 0) {
                    curr = 1;
                } else {
                    // 非边界情况，当前长度 = 左上角值 + 1
                    curr = prev + 1;
                }
                maxLen = max(maxLen, curr);
            } else {
                // 不匹配则当前长度为0
                curr = 0;
            }
            prev = curr;  // 更新prev，供下一列使用
        }
    }
    
    cout << "最长公共字串长度：" << maxLen << endl;
    return 0;
}

Python

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
S = input().strip()
T = input().strip()

n = len(S)
m = len(T)
max_len = 0
prev = 0  # 存储上一轮的dp[i-1][j-1]值

for i in range(n):
    prev = 0  # 每行开始前重置prev
    for j in range(m):
        curr = 0
        if S[i] == T[j]:
            # 边界情况：第一行或第一列，匹配则长度为1
            if i == 0 or j == 0:
                curr = 1
            else:
                # 非边界情况，当前长度 = 左上角值 + 1
                curr = prev + 1
            if curr > max_len:
                max_len = curr
        # 不匹配时curr保持0，无需额外处理
        prev = curr  # 更新prev，供下一列使用

print(f"最长公共字串长度：{max_len}")

如何还原最长公共字串

二维 DP 版肯定也有他的好处，就是记录了这个数组，那么它就被可溯源

  1. 新增两个变量endI和endJ，记录dp[i][j] == maxLen时的 i 和 j；
  2. 最长公共字串的结尾是 S [endI-1]（或 T [endJ-1]），长度为 maxLen；
  3. 从 S 的endI - maxLen位置开始，截取长度为 maxLen 的子串，即为结果。

只需要在二维DP中添加如下内容就可以还原

1
2
3
4
5
6
7
8
9
10
int endI = 0, endJ = 0; // 记录最长字串的结尾位置
// 遍历过程中更新maxLen时，同步记录位置
if (dp[i][j] > maxLen) {
    maxLen = dp[i][j];
    endI = i;
    endJ = j;
}
// 输出最长公共字串
String result = S.substring(endI - maxLen, endI);
System.out.println("最长公共字串：" + result);

例题

问题

P5546 [POI 2000] 公共串

P5546 [POI 2000] 公共串

题目描述

给出几个由小写字母构成的单词，求它们最长的公共子串的长度。

输入格式

文件的第一行是整数 n，1 ≤ n ≤ 5，表示单词的数量。接下来n行每行一个单词，只由小写字母组成，单词的长度至少为1，最大为2000。

输出格式

仅一行，一个整数，最长公共子串的长度。

输入输出样例 #1

输入 #1

1
2
3
4
3
abcb
bca
acbc

输出 #1

1
2

问题分析

这道题要求找出 多个字符串（2~5 个） 中最长的公共子串（连续的相同字符序列）的长度。例如输入的 3 个字符串abcb、bca、acbc，最长公共子串是bc或cb，长度为 2。

与两个字符串的最长公共子串相比，核心区别在于：需要确保子串在 所有 n 个字符串中都出现，而非仅两个。

解决思路我们分两步递进

基础情况就是两个字符串的最长公共子串

先回顾两个字符串的解法（动态规划）：

  • 定义dp[i][j]为以str1[i-1]和str2[j-1]为结尾的最长公共子串长度。
  • 若str1[i-1] == str2[j-1]，则dp[i][j] = dp[i-1][j-1] + 1；否则dp[i][j] = 0。
  • 记录过程中dp[i][j]的最大值，即为答案。

扩展到 n 个字符串的最长公共子串怎么办？

核心思路是 逐步筛选：

  • 先求前两个字符串的所有公共子串，记录这些子串及其长度。
  • 再用这些子串与第三个字符串比对，保留同时存在于第三个字符串中的子串。
  • 重复此过程，直到处理完所有字符串，剩余子串的最大长度即为答案。

但直接存储所有子串会占用大量空间，优化方案是：以最短字符串为基准，枚举其所有可能的子串，检查是否在其他所有字符串中存在。

原因：最长公共子串的长度不可能超过最短字符串的长度，以最短字符串为基准可减少枚举量。

所以，先找到最短字符串，设为s，长度为minLen。

那么这样，最长公共子串的长度最大为minLen。

然后枚举s的所有可能子串

  • 按长度从大到小枚举（一旦找到符合条件的子串，可直接返回其长度，提高效率）。
  • 对于每个长度l（从minLen到 1），枚举所有起始位置i（0 ≤ i ≤ minLen - l），得到子串s.substring(i, i+l)。

检查子串是否在所有其他字符串中存在

  • 若存在，则返回当前长度l（因为按长度从大到小枚举，第一个符合条件的就是最长的）。

若所有长度都检查完仍无结果，返回 0。

编写代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        scanner.nextLine(); // Java21要消费换行符

        // 读取所有字符串
        String[] strs = new String[n];
        for (int i = 0; i < n; i++) {
            strs[i] = scanner.nextLine();
        }

        // 找到最短字符串（减少枚举量）
        int minLen = strs[0].length();
        String shortest = strs[0];
        for (String s : strs) {
            if (s.length() < minLen) {
                minLen = s.length();
                shortest = s;
            }
        }

        // 按长度从大到小枚举最短字符串的所有子串
        for (int l = minLen; l >= 1; l--) { // l是子串长度
            // 枚举所有可能的起始位置
            for (int i = 0; i <= shortest.length() - l; i++) {
                String sub = shortest.substring(i, i + l); // 当前子串
                boolean allContains = true;

                // 检查该子串是否在所有其他字符串中存在
                for (String s : strs) {
                    if (!s.contains(sub)) {
                        allContains = false;
                        break;
                    }
                }

                // 若所有字符串都包含该子串，直接返回长度l
                if (allContains) {
                    System.out.println(l);
                    return;
                }
            }
        }

        // 无公共子串
        System.out.println(0);
    }
}

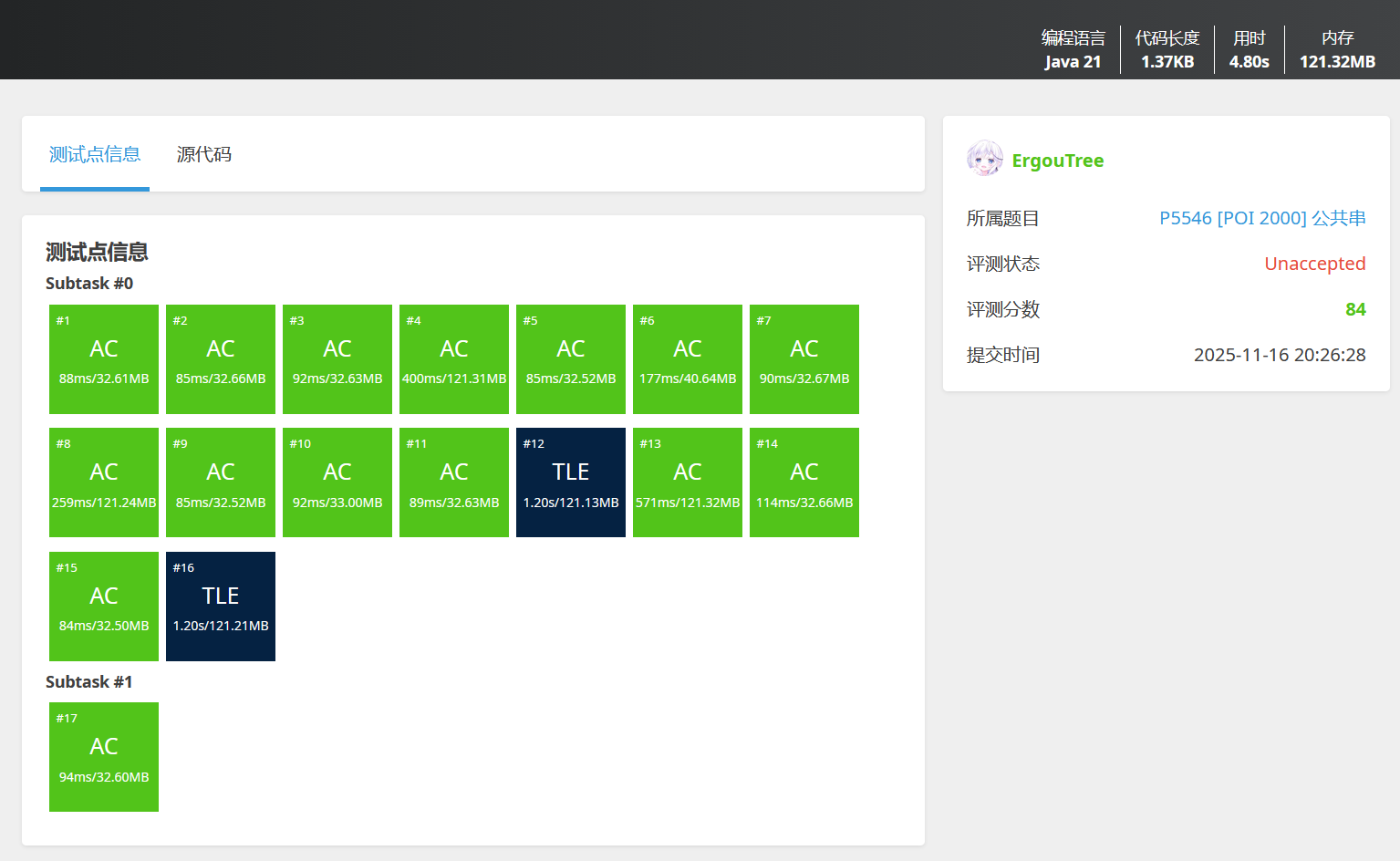image-20251116202649692

很遗憾，燃尽了也只有这个分

因为这个算法下，总时间复杂度是O(L² * n * M)。

所以要通过这个题目，就需要在找串上下手，SAM 后缀自动机是解决多个子串的共同串的好方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
import java.util.Scanner;
import java.util.Arrays;

public class Main {
    static class SAM {
        static class Node {
            int len;      // 该状态表示的最长子串长度
            int link;     // 后缀链接(parent指针)
            int[] next;   // 转移边
            int minMatch; // 在所有字符串中的最小匹配长度
            
            Node() {
                next = new int[26];
                Arrays.fill(next, -1);
                link = -1;
                minMatch = Integer.MAX_VALUE;
            }
        }
        
        Node[] states;
        int size;      // 当前状态数
        int last;      // 最后一个状态
        final int MAXN = 4005; // 最多2*字符串长度个状态
        
        SAM() {
            states = new Node[MAXN];
            for (int i = 0; i < MAXN; i++) {
                states[i] = new Node();
            }
            size = 1;
            last = 0;
            states[0].len = 0;
            states[0].link = -1;
        }
        
        // 添加字符c到SAM
        void extend(char c) {
            int cur = size++;
            states[cur].len = states[last].len + 1;
            
            int p = last;
            while (p != -1 && states[p].next[c - 'a'] == -1) {
                states[p].next[c - 'a'] = cur;
                p = states[p].link;
            }
            
            if (p == -1) {
                states[cur].link = 0;
            } else {
                int q = states[p].next[c - 'a'];
                if (states[p].len + 1 == states[q].len) {
                    states[cur].link = q;
                } else {
                    int clone = size++;
                    states[clone].len = states[p].len + 1;
                    states[clone].link = states[q].link;
                    System.arraycopy(states[q].next, 0, states[clone].next, 0, 26);
                    
                    while (p != -1 && states[p].next[c - 'a'] == q) {
                        states[p].next[c - 'a'] = clone;
                        p = states[p].link;
                    }
                    
                    states[q].link = clone;
                    states[cur].link = clone;
                }
            }
            
            last = cur;
        }
        
        // 用字符串s在SAM上匹配，记录每个状态的最大匹配长度
        void match(String s) {
            int[] curMatch = new int[size]; // 当前字符串在每个状态的匹配长度
            
            int v = 0;      // 当前状态
            int curLen = 0; // 当前匹配长度
            
            for (int i = 0; i < s.length(); i++) {
                int c = s.charAt(i) - 'a';
                
                // 尝试转移
                while (v != 0 && states[v].next[c] == -1) {
                    v = states[v].link;
                    curLen = states[v].len;
                }
                
                if (states[v].next[c] != -1) {
                    v = states[v].next[c];
                    curLen++;
                    curMatch[v] = Math.max(curMatch[v], curLen);
                } else {
                    v = 0;
                    curLen = 0;
                }
            }
            
            // 通过parent树向上传播匹配长度
            // 如果状态v匹配了长度l，那么它的parent也至少能匹配states[parent].len
            for (int i = size - 1; i > 0; i--) {
                if (curMatch[i] > 0 && states[i].link != -1) {
                    int parent = states[i].link;
                    curMatch[parent] = Math.max(curMatch[parent], 
                                                Math.min(curMatch[i], states[parent].len));
                }
            }
            
            // 更新每个状态的最小匹配长度
            for (int i = 0; i < size; i++) {
                states[i].minMatch = Math.min(states[i].minMatch, curMatch[i]);
            }
        }
        
        // 获取所有字符串的最长公共子串长度
        int getAnswer() {
            int ans = 0;
            for (int i = 0; i < size; i++) {
                ans = Math.max(ans, states[i].minMatch);
            }
            return ans;
        }
    }
    
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        sc.nextLine();
        
        String[] strs = new String[n];
        for (int i = 0; i < n; i++) {
            strs[i] = sc.nextLine();
        }
        
        // 构建第一个字符串的SAM
        SAM sam = new SAM();
        for (char c : strs[0].toCharArray()) {
            sam.extend(c);
        }
        
        // 初始化第一个字符串：所有状态的minMatch设为其len
        for (int i = 0; i < sam.size; i++) {
            sam.states[i].minMatch = sam.states[i].len;
        }
        
        // 用其他字符串在SAM上匹配
        for (int i = 1; i < n; i++) {
            sam.match(strs[i]);
        }
        
        System.out.println(sam.getAnswer());
        sc.close();
    }
}
image-20251116203753493