问题

给定 n 种物品和一个容量为 C 的背包。第 i 种物品的重量是 w[i]，价值是 v[i]。

每种物品可以无限次使用（即可以选 0 个、1 个、2 个… 直到背包容量限制）。

问：将哪些物品装入背包，可使这些物品的总重量不超过背包容量，且总价值最大？

image-20251125192750189

问题分析

该问题与 0-1 背包非常像，但是确实是两者问题

  • 0-1 背包：每种物品只能选0 个或 1 个
  • 完全背包：每种物品可以选任意多个

所以，我们依旧可以这样定义状态变量

  • 定义 f[i][j] 表示：考虑前 i 种物品，在背包容量为 j 时的最大价值。

那么接下来就要确定递推关系，那么对当前背包容量 j，依旧考虑的是第i件物品能否放入？或者说是否放入？

所以对于第 i 种物品，我们可以参考 0-1 背包的思路，有多种选择：

  • 选 0 个：dp[i][j] = dp[i-1][j]
    • 也就是当前背包容量 j < w[i]，这个物品放不下
    • 或者能放入，但是不合适，所以不放入
  • 选 1 个：dp[i][j] = dp[i-1][j-w[i]] + v[i]
  • 选 2 个：dp[i][j] = dp[i-1][j-2*w[i]] + 2*v[i]
  • …
  • 选 k 个：dp[i][j] = dp[i-1][j-k*w[i]] + k*v[i]（需满足 k*w[i] ≤ j）

因此，状态转移方程为：

dp[i][j] = max{ dp[i-1][j - k*w[i]] + k*v[i] | 0 ≤ k*w[i] ≤ j }

image-20251125193451294

优化

决策优化

按照上面我的推导，完全背包的原始状态转移方程是：

1
dp[i][j] = max{ dp[i-1][j - k*wei[i]] + k*val[i] | k ≥ 0, k*wei[i] ≤ j }

这里的 k 表示选择第 i 件物品的数量，需要枚举所有可能的 k，时间复杂度为 O(n*m*k)（k 最大为 j/wei[i]），效率较低。

那么这个优化很好思考，如果我们把物品都考虑成个数，那么整个循环就需要多出一重对物品个数的循环

不如改成对其整体体积的循环，将枚举 k 的过程化简为两次状态比较，从而将时间复杂度降到 O(n*m)。

  • 对于dp[i][j]，考虑选 0 个或多个第i件物品：
    • 选 0 个：dp[i][j] = dp[i-1][j]
    • 选至少 1 个：可以先选 1 个第 i 件物品，剩下的容量 j-wei[i] 仍然可以选第 i 件物品，即 dp[i][j] = dp[i][j-wei[i]] + val[i]

因此，优化后的状态转移方程为：

1
dp[i][j] = max(dp[i-1][j], dp[i][j-wei[i]] + val[i])

要么不选第 i 个物品，用前 i-1 个物品的结果 dp[i-1][j]；要么选第 i 个物品，此时可以重复选，所以结果都是用当前物品已选过的状态 dp[i][j - w[i]]」+ 价值 v[i] 进行推导得到的

也就是说，别管放几个，完全背包是任意多个，只要我想，而且背包可以，我可以一直放

背包能放前 i 个，下一轮去比体积还是够，那么我就可以放入第 i+1 个

k 就不用枚举了。

空间优化

思考0-1背包都可以滚动优化掉一维，所以完全背包是否也可以

我们可以考虑将二维数组优化为一维数组 dp[j]，表示容量为 j 的背包的最大价值

单元格依旧是靠前面推出来的，靠前面的加上其重量，价值也是这样加

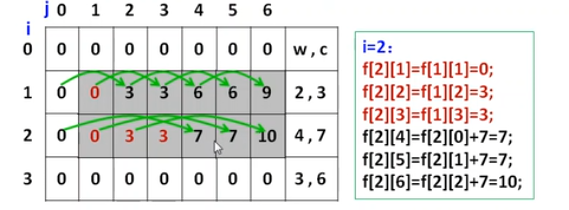image-20251125193825079

某个单元格可以从列变量的差值进行推导

二维数组中，dp[i][j] 只依赖上一行的 dp[i-1][...] 和当前行的 dp[i][...] —— 这意味着我们可以用「同一个数组」覆盖更新，不需要额外存储前 i-1 行的所有数据。

用一维数组 f[j]只记录一行数据，让 j 值循环，顺序更新 f[j] 值

image-20251125195402772

那么完全背包的遍历逻辑是不一样的

在0-1 背包中，一维数组的内层循环是从后往前遍历容量，这是为了，我在装的下的时候，如果选择装，就赶紧装（从后往前遍历容量），然后进入对下一个物品的决策，这是为了什么呢？其实就是避免重复选物品

而完全背包是可以重复选择物品的，所以一维数组的内层循环是从前往后遍历容量

  • 0-1 背包：dp[j] 依赖于 dp[j-w[i]] 的旧值（上一轮的结果），所以必须从后往前
  • 完全背包：dp[j] 可以依赖于 dp[j-w[i]] 的新值（本轮的结果），这正好体现了 “可以重复选择” 的特性

那么状态转移方程就变成如下

1
dp[j] = max(dp[j], dp[j - w[i]] + v[i])

最后分析一下时空复杂度

  • 时间复杂度：O(n*C)，其中 n 是物品数量，C 是背包容量
  • 空间复杂度：O(C)（优化后的一维数组解法）

代码

基础版本

此时就可以给出最基础的代码

策略为枚举个数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
// 完全背包一般是物品有无限多件，然后求最大价值
// 01背包中第i件物品可以放入0个或1个
// 而完全背包可以放入任意数个

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        int m = scanner.nextInt();
        int[] val = new int[n + 1];
        int[] wei = new int[n + 1];
        // 最大价值是dp[i][j]前i件物品放入容量为j的背包的最大价值的函数关系
        int[][] dp = new int[1010][1010];

        for (int i = 1; i <= n; i++) {
            wei[i] = scanner.nextInt();
            val[i] = scanner.nextInt();
        }

        for (int i = 1; i <= n; i++)       //阶段：枚举物品
            for (int j = 0; j <= m; j++)       //状态：枚举体积
                for (int k = 0; k <= j / wei[i]; k++)  //决策：枚举个数
                    dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - wei[i] * k] + val[i] * k);

        System.out.println(dp[n][m]);

        scanner.close();
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
// 朴素算法 TLE
#include <iostream>
#include <algorithm>
using namespace std;

const int N=1010;
int n, m;
int v[N], w[N];
int f[N][N];

int main(){
  scanf("%d%d",&n,&m);
  for(int i=1; i<=n; i++) 
    scanf("%d%d",&v[i],&w[i]);  //费用，价值
  
  for(int i=1; i<=n; i++)       //阶段：枚举物品
  for(int j=0; j<=m; j++)       //状态：枚举体积
  for(int k=0; k<=j/v[i]; k++)  //决策：枚举个数
    f[i][j]=max(f[i][j], f[i-1][j-v[i]*k]+w[i]*k);
  
  printf("%d\n",f[n][m]);
}

决策优化

策略为枚举体积

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        int m = scanner.nextInt();
        int[] val = new int[n + 1];
        int[] wei = new int[n + 1];
        // 最大价值是dp[i][j]前i件物品放入容量为j的背包的最大价值的函数关系
        int[][] dp = new int[1010][1010];

        for (int i = 1; i <= n; i++) {
            wei[i] = scanner.nextInt();
            val[i] = scanner.nextInt();
        }

        for (int i = 1; i <= n; i++)       //枚举物品
            for (int j = 1; j <= m; j++)     //枚举体积
                // 第i件物品不能放入背包
                if (j < wei[i]) dp[i][j] = dp[i - 1][j];
                // 第i件物品能放入背包，需要比较放入和不放入的代价
                // 对于前i件物品，由于背包容量j-w[i]的时候可能已经放入了第i件物品，容量为j的时候还可以放入，所以用f[i][j-w[i]]更新f[i][j]
                else dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - wei[i]] + val[i]);

        System.out.println(dp[n][m]);

        scanner.close();
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
// 优化决策
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int N=1010;
int n, m;
int v[N],w[N],f[N][N];

int main(){
  scanf("%d%d",&n,&m);
  for(int i=1; i<=n; i++) 
    scanf("%d%d",&v[i],&w[i]);  //费用，价值
  
  for(int i=1; i<=n; i++)       //枚举物品
    for(int j=1; j<=m; j++)     //枚举体积
      if(j<v[i]) f[i][j]=f[i-1][j];
      else f[i][j]=max(f[i-1][j],f[i][j-v[i]]+w[i]);         
      
  printf("%d\n",f[n][m]);
}

决策优化加优化空间

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        int m = scanner.nextInt();
        int[] val = new int[n + 1];
        int[] wei = new int[n + 1];
        // 用一维数组只记录一行数据，让j顺序循环顺序更新，滚动掉一维
        int[] dp = new int[1010];

        for (int i = 1; i <= n; i++) {
            wei[i] = scanner.nextInt();
            val[i] = scanner.nextInt();
        }

        for (int i = 1; i <= n; i++) {   // 枚举物品
            // 顺序枚举j，新数值f[j-w[i]]会先于f[j]更新，是正确的
            for (int j = wei[i]; j <= m; j++) {  // 枚举容量
                dp[j] = Math.max(dp[j], dp[j - wei[i]] + val[i]);
            }
        }

        System.out.println(dp[m]);

        scanner.close();
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
// 优化决策+滚动数组优化空间
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int N=1010;
int n, m;
int v[N],w[N],f[2][N];

int main(){
  scanf("%d%d",&n,&m);
  for(int i=1; i<=n; i++) 
    scanf("%d%d",&v[i],&w[i]);  //费用，价值
  
  for(int i=1; i<=n; i++)       //枚举物品
    for(int j=1; j<=m; j++)     //枚举体积
      if(j<v[i]) f[i&1][j]=f[i-1&1][j];
      else f[i&1][j]=max(f[i-1&1][j],f[i&1][j-v[i]]+w[i]);         
      
  printf("%d\n",f[n&1][m]);
}

过渡例题

问题

[P13957 ICPC 2023 Nanjing R 背包][https://www.luogu.com.cn/problem/P13957]

P13957 [ICPC 2023 Nanjing R] 背包

题目描述

小青鱼，一位没有经验的商人，最近开了一家名叫“皇后有机珠宝”（QOJ）的店。这家珠宝店共有 n 枚宝石，其中第 i 枚售价为 wi 元，美丽度为 vi。进入商店之前，您准备了 W 元用来买下美丽度总和尽量高的宝石。

有趣的是，小青鱼的店今天正在促销。任何顾客都可以任选 k 枚宝石并免费获得它们。有了这样的机会，您很想知道，如果您使用最佳策略，用 W 元到底能获得美丽度总和多高的宝石。

请注意，每枚宝石独此一份，您不能多次获取同一枚宝石。另外，您无需花完所有的钱。

输入格式

每个测试文件仅有一组测试数据。

第一行输入三个整数 n，W 和 k（1 ≤ n ≤ 5 × 103，1 ≤ W ≤ 104，0 ≤ k ≤ n），表示商店中宝石的总数，您拥有的金钱数以及您可以免费获得的宝石数量。

对于接下来 n 行，第 i 行输入两个整数 wi 和 vi（1 ≤ wi ≤ W，1 ≤ vi ≤ 109），表示第 i 枚宝石的售价和美丽度。

输出格式

输出一行一个整数表示答案。

输入输出样例 #1

输入 #1

1
2
3
4
5
4 10 1
9 10
10 1
3 5
5 20

输出 #1

1
35

输入输出样例 #2

输入 #2

1
2
3
4
5
6
5 13 2
5 16
5 28
7 44
8 15
8 41

输出 #2

1
129

说明/提示

对于第一组样例数据，小青鱼的商店有 4 枚宝石，您可以免费获得其中 1 枚。一种最优策略是免费获取第一枚宝石，并购买第三和第四枚宝石。

$$\begin{array}{ | c | c | c | c | } \hline \bf{宝石} & \bf{售价 w_i} & \bf{美丽度 v_i} & \bf{操作} \\ \hline 1 & 9 & 10 & 免费获取 \\ \hline 2 & 10 & 1 & / \\ \hline 3 & 3 & 5 & 购买 \\ \hline 4 & 5 & 20 & 购买 \\ \hline \end{array}$$

所以答案是 10 + 5 + 20 = 35。

问题分析

这是一个 0-1 背包问题，因为每枚宝石只能选一次

为什么完全背包要做 0-1 背包的问题呢？

因为他和完全背包的思路，比较像

首先，这道题的核心是：

  • 每枚宝石只能选一次（0-1 背包特性）
  • 可以免费选 k 枚宝石
  • 剩下的宝石需要花钱买，总花费不超过 W
  • 目标是最大化总美丽度

那么如何最大化总美丽度呢？（价值）

既然能免费拿，肯定免费拿贵的，而且是被免费带走的物品应该是价格（体积）比较大的物品

那为了求最大可以获得的数量，一定要将这 k 次机会使用掉，那么问题就是该怎么最大效益的用:

  • 用于最贵的 k 个。
  • 用于所得美丽度最大的 k 个。

因此，最优策略是：将物品按体积从小到大排序，然后从后（体积大的物品）往前选 k 个价值最高的物品免费拿。

贪心

首先要排序，将所有物品按体积（价格）v从小到大排序。这样体积大的物品集中在数组后面。

然后定义并处理一个sum[i]，表示从第 i 个物品到最后一个物品中，免费选 k 个价值最高的物品的总价值。

  • 从后往前遍历物品，维护一个大根堆（或排序数组）记录当前物品之后的所有物品价值
  • 每次取前 k 个最大的价值求和，存入 sum [i]

再对前 i 个物品（体积较小的物品）做 0-1 背包，计算在预算 W 下能获得的最大价值，存入f[i][j]。

由于售价更高相比于售价低的成为背包最优解的可能更低，于是想到将前缀做背包，后缀零元购取美丽度最高的几个。

所以，遍历所有可能的分割点 i

  • 前 i 个物品用 DP 计算最大价值（花钱买）
  • i+1 到 n 个物品中选 k 个价值最高的免费拿（sum [i+1]）
  • 两者之和的最大值就是答案

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
import java.util.*;
import java.io.*;

public class Main {

    static class Node implements Comparable<Node> {
        int w, v;  // w是价格（体积），v是价值（美丽度）

        public Node(int w, int v) {
            this.w = w;
            this.v = v;
        }

        @Override
        public int compareTo(Node o) {
            return Integer.compare(this.w, o.w);  // 按价格从小到大排序
        }
    }

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        int n = Integer.parseInt(st.nextToken());
        int W = Integer.parseInt(st.nextToken());
        int k = Integer.parseInt(st.nextToken());

        Node[] nodes = new Node[n + 1];
        for (int i = 1; i <= n; i++) {
            st = new StringTokenizer(br.readLine());
            int w = Integer.parseInt(st.nextToken());   // 售价
            int v = Integer.parseInt(st.nextToken());   // 美丽度
            nodes[i] = new Node(w, v);
        }

        // 美丽度从小到大排序
        Arrays.sort(nodes, 1, n + 1);

        // 然后处理sum数组
        // sum[i]表示i到n中选k个最大价值的和
        long[] sum = new long[n + 2];
        List<Integer> p = new ArrayList<>();

        // 倒序选择美丽度大的
        for (int i = n; i >= 1; i--) {
            p.add(nodes[i].v);
            // 降序排序
            p.sort(Collections.reverseOrder());

            int size = p.size();
            long sum_c = 0;
            int take = Math.min(k, size);
            for (int j = 0; j < take; j++) {
                sum_c += p.get(j);
            }
            sum[i] = sum_c;
        }

        // 0-1 背包dp
        long[][] dp = new long[n + 1][W + 1];

        for (int i = 1; i <= n; i++) {
            // 不选第i个物品
            System.arraycopy(dp[i - 1], 0, dp[i], 0, W + 1);

            // 选第i个物品
            int wi = nodes[i].w;
            int vi = nodes[i].v;
            // 倒序01背包，体积倒序
            for (int j = W; j >= wi; j--) {
                dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - wi] + vi);
            }
        }

        // 找最优解
        long res = 0;
        for (int i = 0; i <= n; i++) {
            res = Math.max(res, dp[i][W] + sum[i + 1]);
        }

        System.out.println(res);
    }
}

image-20251125202407093

真 例题

问题

[P2347 [NOIP 1996 提高组] 砝码称重][https://www.luogu.com.cn/problem/P2347]

P2347 [NOIP 1996 提高组] 砝码称重

题目描述

设有 1g、2g、3g、5g、10g、20g 的砝码各若干枚（其总重 $ $），可以表示成多少种重量？

输入格式

输入方式：a1, a2, a3, a4, a5, a6

（表示 1g 砝码有 a1 个，2g 砝码有 a2 个，…，20g 砝码有 a6 个）

输出格式

输出方式：Total=N

（N 表示用这些砝码能称出的不同重量的个数，但不包括一个砝码也不用的情况）

输入输出样例 #1

输入 #1

1
1 1 0 0 0 0

输出 #1

1
Total=3

说明/提示

【题目来源】

NOIP 1996 提高组第四题

问题分析

这道题要求计算：用给定数量的不同重量砝码，能组成多少种不同的总重量。

  • 有6种砝码：1g, 2g, 3g, 5g, 10g, 20g
  • 每种砝码数量有限（不是无限的）
  • 求能组成的不同重量的种数（不是方案数）

这是完全背包吗？

我认为这个虽然很像多重背包，但是，它这题有个特殊性，我们不关心”最大价值”，只关心”能达到哪些重量”。

定义 dp[w] 为 是否能凑出重量 w

题目就转换成了统计有多少个 dp[w] = true

对于每种砝码，我们可以选择用 0 个、1 个、2 个…直到该砝码的数量上限。

状态转移可以这样思考

  • 对于第 i 种砝码（重量为weight[i]，数量为 count[i]）：
    • 对于每个可能的重量 w：
      • 对于使用 k 个该砝码（0 ≤ k ≤ count[i]）
        • 如果 dp[w - k * weight[i]] 为 true，则 dp[w] = true

关键是我们要从小到大遍历重量

为什么？因为我们要避免”重复使用”同一个砝码。如果从小到大遍历，更新 dp[w] 后，它会影响到 dp[w + weight] 的计算，导致同一个砝码被多次使用。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);

        // 砝码重量
        int[] weights = {1, 2, 3, 5, 10, 20};
        // 每种砝码的数量
        int[] counts = new int[6];

        // 读入数据，计算总重量
        int totalWeight = 0;
        for (int i = 0; i < 6; i++) {
            counts[i] = sc.nextInt();
            totalWeight += weights[i] * counts[i];
        }

        // dp[w] 表示能否凑出重量 w
        boolean[] dp = new boolean[totalWeight + 1];
        dp[0] = true; // 初始状态：0 重量可以凑出（不选任何砝码）

        // 枚举每种砝码
        for(int i = 0; i < 6; i++){
            int weight = weights[i];
            int count = counts[i];

            for (int w = totalWeight; w >= weight; w--) {
                // 枚举当前使用的砝码是多重
                for(int k = 1; k < count && k * weight <= w; k++){
                    // 可以被称出加上这个砝码前的重量，那么这个也可以被称出
                    if (dp[w - k * weight]) {
                        dp[w] = true;
                    }
                }
            }
        }
    }
}

image-20251125204157775

变形

[P1441 砝码称重][https://www.luogu.com.cn/problem/P1441]

从 n 个砝码中选择去掉 m 个该如何做呢？

多一个 DFS，从 n 个砝码中选择去掉 m 个 ，就需要枚举所有可能的删除方案，枚举删除哪些

对剩余的砝码，计算能称出多少种重量，也就是 0-1背包

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
import java.util.Scanner;

public class Main {
    static int n, m;
    static int[] a;           // 砝码重量
    static boolean[] tf;      // 标记数组：tf[i]=true表示第i个砝码被删除
    static boolean[] f;       // DP数组：f[w]=true表示能称出重量w
    static int maxResult = 0; // 全局最优答案
    
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        n = sc.nextInt();
        m = sc.nextInt();
        
        a = new int[n];
        tf = new boolean[n];
        f = new boolean[2010];
        
        for (int i = 0; i < n; i++) {
            a[i] = sc.nextInt();
        }
        
        dfs(0, 0);
        
        System.out.println(maxResult);
        sc.close();
    }
    
    /**
     * DFS枚举删除方案
     
     * @param cur 当前考虑第几个砝码（0-based）
     * @param now 当前已删除的砝码数量
     */
    static void dfs(int cur, int now) {
        // 剪枝：删除数量超过m，直接返回
        if (now > m) return;
        
        // 边界：遍历完所有砝码
        if (cur == n) {
            if (now == m) {  // 恰好删除m个，执行DP
                dp();
            }
            return;
        }
        
        // 选择1：不删除当前砝码
        dfs(cur + 1, now);
        
        // 选择2：删除当前砝码
        tf[cur] = true;
        dfs(cur + 1, now + 1);
        tf[cur] = false;  // 回溯
    }
    
    /**
     * 使用0-1背包计算能称出多少种重量
     */
    static void dp() {
        // 初始化
        for (int i = 0; i < f.length; i++) {
            f[i] = false;
        }
        f[0] = true;
        
        int ans = 0;   // 当前方案能称出的重量种数
        int tot = 0;   // 当前最大可能重量
        
        // 枚举每个砝码
        for (int i = 0; i < n; i++) {
            if (tf[i]) continue;  // 跳过被删除的砝码
            
            // 倒序遍历（0-1背包）
            // 只遍历到tot
            for (int j = tot; j >= 0; j--) {
                // 只在第一次变为true时计数
                if (f[j] && !f[j + a[i]]) {
                    f[j + a[i]] = true;
                    ans++;  // 边DP边统计
                }
            }
            
            tot += a[i];  // 更新最大可能重量
        }
        
        maxResult = Math.max(maxResult, ans);
    }
}
image-20251125205022994

可见完全背包的问题可以被藏成很多情况