问题

单调队列是一种很典型的问题，它能用来高效地解决 “滑动窗口最大值” 问题的数据结构

给定一个长度为 n 的数组 nums 和一个大小为 k 的滑动窗口，窗口从数组左端向右滑动，每次滑动一格，求每个窗口内的最大（小）值。

那么这种问题大概率其实下意识会想到用堆

如果是求最大值，但是如果使用大根堆，每次插入 O (logk)，但删除窗口左侧元素，也就是删除不在窗口内的堆顶的时候，需要 O (n)，整体 O (nlogk)，仍不够高效。

P1886 滑动窗口 /【模板】单调队列 - 洛谷

P1886 滑动窗口 /【模板】单调队列

题目描述

有一个长为 n 的序列 a，以及一个大小为 k 的窗口。现在这个窗口从左边开始向右滑动，每次滑动一个单位，求出每次滑动后窗口中的最小值和最大值。

例如，对于序列 [1, 3, −1, −3, 5, 3, 6, 7] 以及 k = 3，有如下过程：

$$\def\arraystretch{1.2} \begin{array}{|c|c|c|}\hline \textsf{窗口位置} & \textsf{最小值} & \textsf{最大值} \\ \hline \verb![1 3 -1] -3 5 3 6 7 ! & -1 & 3 \\ \hline \verb! 1 [3 -1 -3] 5 3 6 7 ! & -3 & 3 \\ \hline \verb! 1 3 [-1 -3 5] 3 6 7 ! & -3 & 5 \\ \hline \verb! 1 3 -1 [-3 5 3] 6 7 ! & -3 & 5 \\ \hline \verb! 1 3 -1 -3 [5 3 6] 7 ! & 3 & 6 \\ \hline \verb! 1 3 -1 -3 5 [3 6 7]! & 3 & 7 \\ \hline \end{array} $$

输入格式

输入一共有两行，第一行有两个正整数 n, k；
第二行有 n 个整数，表示序列 a。

输出格式

输出共两行，第一行为每次窗口滑动的最小值；
第二行为每次窗口滑动的最大值。

输入输出样例 #1

输入 #1

1
2
8 3
1 3 -1 -3 5 3 6 7

输出 #1

1
2
-1 -3 -3 -3 3 3
3 3 5 5 6 7

说明/提示

【数据范围】
对于 50% 的数据，1 ≤ n ≤ 105；
对于 100% 的数据，1 ≤ k ≤ n ≤ 106，ai ∈ [−231, 231)。

问题分析

以求滑动窗口内最小值为例子

单调队列是什么？

单调队列用一个双向队列（deque） 维护窗口内的元素，队列满足 “从队头到队尾单调递增”

  • 队头永远是当前窗口的最小值；
  • 新元素入队时，删除队列尾部所有比它大的元素，因为这些元素不可能成为后续窗口的最小值；（删掉大的，留下小的，维护队列有效性）
  • 窗口滑动时，若队头元素是窗口左侧要移除的元素，则将其出队。

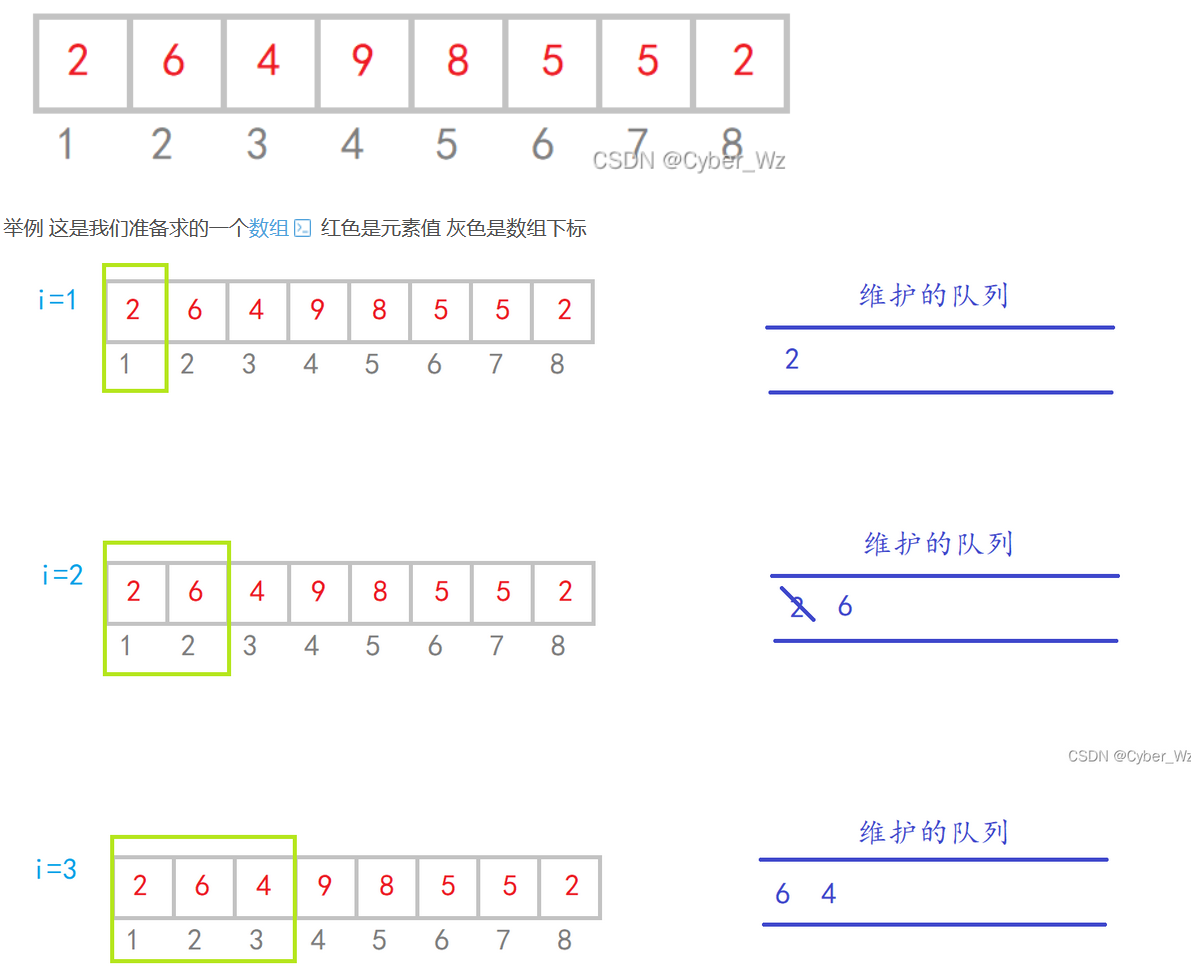
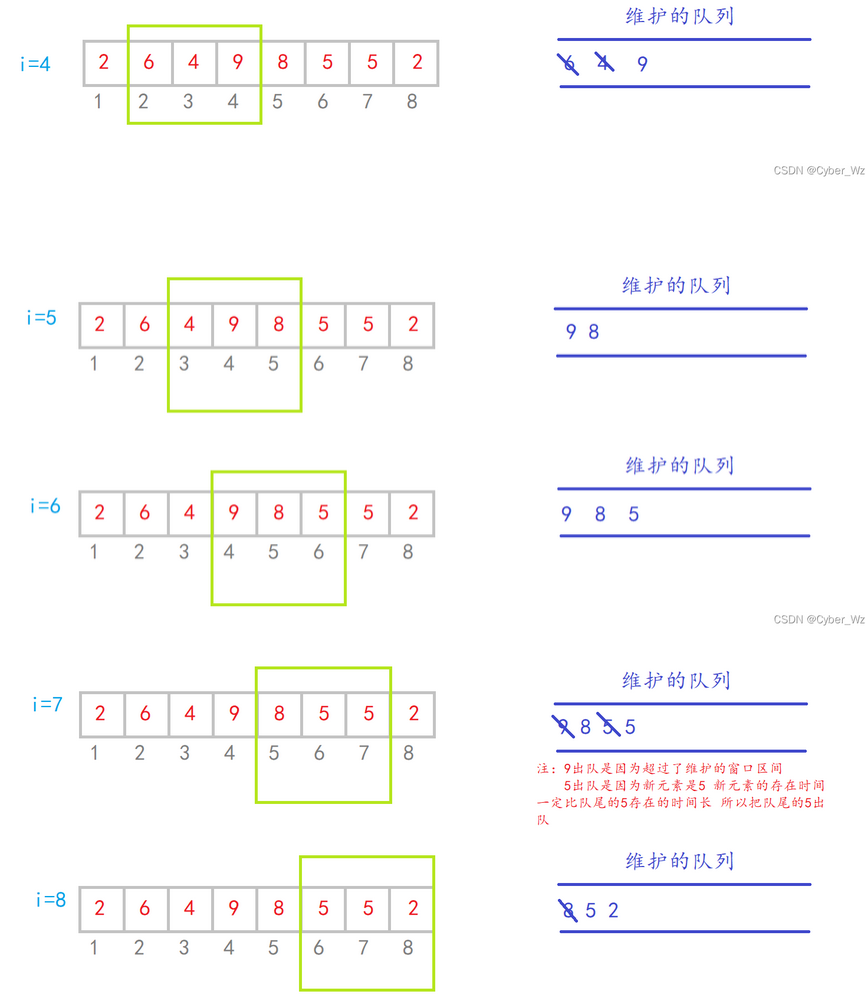
先不说那抽象的入队规则，我们看一个例子，例如

nums = [1,3,-1,-3,5,3,6,7]，滑动窗口大小k=3，求每个窗口的最小值

双向队列deque一般是存下标的

  1. 处理nums[0] = 1（下标 0）：
    • 队列空，直接入队 → deque = [0]（队列内下标对应的值：[1]）；
  2. 处理nums[1] = 3（下标 1）：
    • 队尾元素值1 < 3，满足单调递增，直接入队 → deque = [0,1]（对应值：[1,3]）；
  3. 处理nums[2] = -1（下标 2）：
    • 队尾元素值3 > -1 → 删除下标 1；
    • 新队尾元素值1 > -1 → 删除下标 0；
    • 队列空，入队 → deque = [2]（对应值：[-1]）；
  4. 第一个窗口（下标 0-2）处理完毕，队头是 2，对应值-1 → res[0] = -1。

然后按照这样的思路，处理下标 3 到 7，共 5 个元素，对应 5 个窗口，每个元素处理遵循「出队→入队→记录结果」三步

  • 窗口 1：下标 1-3（元素 [3,-1,-3]）→ 处理nums[3] = -3（下标 3）
    1. 出队检查：窗口左边界 = 3-3+1 = 1，队头下标 2 ≥ 1（在窗口内），无需出队；
    2. 入队维护：队尾元素值-1 > -3 → 删除下标 2；队列空，入队 → deque = [3]（对应值：[-3]）；
    3. 记录结果：i=3 ≥ k-1=2，res[1] = nums[3] = -3。
  • 窗口 2：下标 2-4（元素 [-1,-3,5]）→ 处理nums[4] = 5（下标 4）
    1. 出队检查：窗口左边界 = 4-3+1=2，队头下标 3 ≥2（在窗口内），无需出队；
    2. 入队维护：队尾元素值-3 <5，满足递增，直接入队 → deque = [3,4]（对应值：[-3,5]）；
    3. 记录结果：res[2] = nums[3] = -3。
  • 窗口 3：下标 3-5（元素 [-3,5,3]）→ 处理nums[5] = 3（下标 5）
    1. 出队检查：窗口左边界 = 5-3+1=3，队头下标 3 ≥3（在窗口内），无需出队；
    2. 入队维护：队尾元素值5 >3 → 删除下标 4；新队尾元素值-3 <3，入队 → deque = [3,5]（对应值：[-3,3]）；
    3. 记录结果：res[3] = nums[3] = -3。
  • 窗口 4：下标 4-6（元素 [5,3,6]）→ 处理nums[6] =6（下标 6）
    1. 出队检查：窗口左边界 = 6-3+1=4，队头下标 3 <4（已出窗）→ 出队；新队头下标 5 ≥4（在窗口内）；
    2. 入队维护：队尾元素值3 <6，满足递增，直接入队 → deque = [5,6]（对应值：[3,6]）；
    3. 记录结果：res[4] = nums[5] =3。
  • 窗口 5：下标 5-7（元素 [3,6,7]）→ 处理nums[7] =7（下标 7）
    1. 出队检查：窗口左边界 = 7-3+1=5，队头下标 5 ≥5（在窗口内），无需出队；
    2. 入队维护：队尾元素值6 <7，满足递增，直接入队 → deque = [5,6,7]（对应值：[3,6,7]）；
    3. 记录结果：res[5] = nums[5] =3。

最终结果

res = [-1, -3, -3, -3, 3, 3]

这次我们再看单调队列更新数据的规则

  1. 队头元素：取当前滑动窗口的最小值
  2. 入队规则：新元素为了入队，它必须保证没有比它大的，就要删除队列尾部所有「比当前元素大」的元素
    • 大元素在当前元素存在时，永远不可能成为后续窗口的最小值，因为当前元素更小，它会更晚被移出窗口
  3. 出队规则：窗口向右滑动时，若队头元素是窗口左侧要移除的元素（已不在窗口内），则将其从队头出队
    • 确保队头元素始终在当前窗口中
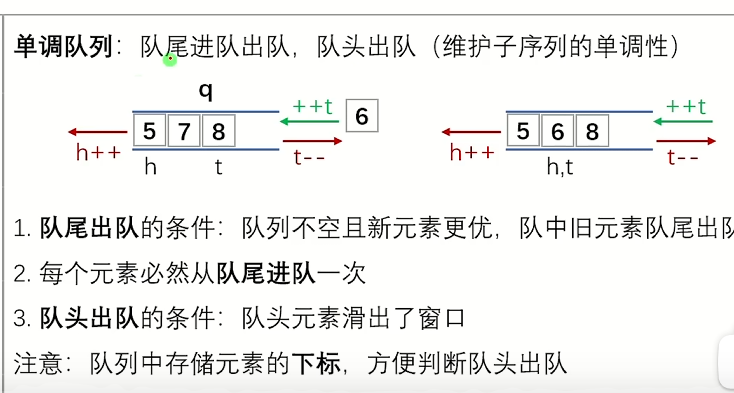
image-20251117204647673

为什么单调队列要存下标，而不是元素值

因为单调队列比数大小这一步，他不在单调队列的内部进行，而出队规则是要判断下标，在单调队列内部进行，所以队列中存储的是「数组元素的下标」，而非元素值，它的目的是方便判断元素是否在当前窗口内，通过下标对比窗口边界。

image-20251117204535398
image-20251117204553212

模板代码

Java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
import java.io.*;
import java.util.*;

// 更清晰的单调队列实现
class MonotonicQueue {
    private int n, k;
    private int[] arr;
    
    public MonotonicQueue(int n, int k, int[] arr) {
        this.n = n;
        this.k = k;
        this.arr = arr;
    }
    
    // 求滑动窗口最小值
    public void getMinValues() throws IOException {
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        Deque<Integer> deque = new ArrayDeque<>(); // 存储下标
        
        for (int i = 0; i < n; i++) {
            // 队列不空且新元素更优，队尾出队，移除队列中所有大于当前元素的元素，保持队列递增
            while (!deque.isEmpty() && arr[deque.peekLast()] >= arr[i]) {
                deque.pollLast();
            }
            
            // 将当前元素下标加入队列
            deque.offerLast(i);
            
            // 移除超出窗口范围的元素
            if (!deque.isEmpty() && deque.peekFirst() <= i - k) {
                deque.pollFirst();
            }
            
            // 当窗口形成时输出最小值
            if (i >= k - 1) {
                bw.write(arr[deque.peekFirst()] + " ");
            }
        }
        bw.newLine();
        bw.flush();
    }
    
    // 求滑动窗口最大值
    public void getMaxValues() throws IOException {
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        Deque<Integer> deque = new ArrayDeque<>(); // 存储下标
        
        for (int i = 0; i < n; i++) {
            // 移除队列中所有小于当前元素的元素，保持队列递减
            while (!deque.isEmpty() && arr[deque.peekLast()] <= arr[i]) {
                deque.pollLast();
            }
            
            // 将当前元素下标加入队列
            deque.offerLast(i);
            
            // 移除超出窗口范围的元素
            if (!deque.isEmpty() && deque.peekFirst() <= i - k) {
                deque.pollFirst();
            }
            
            // 当窗口形成时输出最大值
            if (i >= k - 1) {
                bw.write(arr[deque.peekFirst()] + " ");
            }
        }
        bw.newLine();
        bw.flush();
    }
}

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        String[] firstLine = br.readLine().split(" ");
        int n = Integer.parseInt(firstLine[0]);
        int k = Integer.parseInt(firstLine[1]);
        
        int[] arr = new int[n];
        String[] secondLine = br.readLine().split(" ");
        for (int i = 0; i < n; i++) {
            arr[i] = Integer.parseInt(secondLine[i]);
        }
        
        MonotonicQueue mq = new MonotonicQueue(n, k, arr);
        mq.getMinValues();
        mq.getMaxValues();
    }
}

c++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
#include <iostream>
#include <cstdio>
using namespace std;

const int MAXN = 1e6 + 10; 
int arr[MAXN];
int queue[MAXN]; // 模拟单调队列（存下标）
int n, k;

// 滑动窗口最小值（单调递增队列）
void getMin() {
    int head = 1, tail = 0;
    for (int i = 1; i <= n; ++i) {
        // 维护队列单调性：删除队尾比当前元素大的元素
        while (head <= tail && arr[queue[tail]] >= arr[i]) {
            tail--;
        }
        // 当前元素下标入队
        queue[++tail] = i;
        // 移除窗口外的队头元素
        if (queue[head] < i - k + 1) {
            head++;
        }
        // 窗口形成后输出
        if (i >= k) {
            printf("%d ", arr[queue[head]]);
        }
    }
    printf("\n");
}

// 滑动窗口最大值（单调递减队列）
void getMax() {
    int head = 1, tail = 0;
    for (int i = 1; i <= n; ++i) {
        // 维护队列单调性：删除队尾比当前元素小的元素
        while (head <= tail && arr[queue[tail]] <= arr[i]) {
            tail--;
        }
        // 当前元素下标入队
        queue[++tail] = i;
        // 移除窗口外的队头元素
        if (queue[head] < i - k + 1) {
            head++;
        }
        // 窗口形成后输出
        if (i >= k) {
            printf("%d ", arr[queue[head]]);
        }
    }
    printf("\n");
}

int main() {
    // 快读优化（适配大数据）
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    
    cin >> n >> k;
    for (int i = 1; i <= n; ++i) {
        cin >> arr[i];
    }
    
    getMin();
    getMax();
    
    return 0;
}

python

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
from collections import deque
import sys

def main():
    # 快读：适配大数据输入
    input = sys.stdin.read().split()
    idx = 0
    n = int(input[idx])
    idx += 1
    k = int(input[idx])
    idx += 1
    arr = list(map(int, input[idx:idx+n]))
    
    # 滑动窗口最小值（单调递增队列）
    def get_min():
        q = deque()
        res = []
        for i in range(n):
            # 维护队列单调性：删除队尾比当前元素大的元素
            while q and arr[q[-1]] >= arr[i]:
                q.pop()
            # 当前元素下标入队
            q.append(i)
            # 移除窗口外的队头元素
            while q[0] < i - k + 1:
                q.popleft()
            # 窗口形成后记录结果
            if i >= k - 1:
                res.append(str(arr[q[0]]))
        print(' '.join(res))
    
    # 滑动窗口最大值（单调递减队列）
    def get_max():
        q = deque()
        res = []
        for i in range(n):
            # 维护队列单调性：删除队尾比当前元素小的元素
            while q and arr[q[-1]] <= arr[i]:
                q.pop()
            # 当前元素下标入队
            q.append(i)
            # 移除窗口外的队头元素
            while q[0] < i - k + 1:
                q.popleft()
            # 窗口形成后记录结果
            if i >= k - 1:
                res.append(str(arr[q[0]]))
        print(' '.join(res))
    
    get_min()
    get_max()

if __name__ == "__main__":
    main()

例题

题目

[P1440 求m区间内的最小值][https://www.luogu.com.cn/problem/P1440]

P1440 求m区间内的最小值

题目描述

一个含有 n 项的数列，求出每一项前的 m 个数到它这个区间内的最小值。若前面的数不足 m 项则从第 1 个数开始，若前面没有数则输出 0。

输入格式

第一行两个整数，分别表示 n，m。

第二行，n 个正整数，为所给定的数列 ai。

输出格式

n 行，每行一个整数，第 i 个数为序列中 ai 之前 m 个数的最小值。

输入输出样例 #1

输入 #1

1
2
6 2
7 8 1 4 3 2

输出 #1

1
2
3
4
5
6
0
7
7
1
1
3

说明/提示

对于 100% 的数据，保证 1 ≤ m ≤ n ≤ 2 × 106，1 ≤ ai ≤ 3 × 107。

问题分析

题目要求对数列第 i 项（从 1 开始计数），求「前 m 个元素到它」的最小值，特殊情况：

  • 第 1 项（i=1）：前面没有元素 → 输出 0；
  • 第 2~m 项（i≤m）：前面不足 m 个元素 → 窗口是「第 1 项到第 i-1 项」；
  • 第 m+1 项及以后（i>m）：窗口是「第 i-m 项到第 i-1 项」（固定大小 m 的滑动窗口）。

本质是「动态窗口的最小值问题」。窗口右边界是 “第 i-1 项”，左边界是 “max (1, i-m)”，求这个窗口的最小值。

这和上面滑动窗口最小值的区别就在于，左边窗口的大小是可变的，是 m

所以规则也是一样的

  • 入队规则：新元素（当前处理的 a [j]）入队前，删除队尾所有「比它大」的元素 —— 这些大元素不可能成为后续窗口的最小值；
  • 出队规则：窗口左边界右移时（i>m），若队头下标 < 左边界（i-m），则队头出队 —— 确保队头元素在当前窗口内。

那么对第 i 项的答案（i从 1 到 n），窗口是「max (1, i-m)到 i-1」，对应处理 j=i-1 时，左边界为 max (1, i-m) = max (1, (j+1)-m)。

那么特殊情况就是这样

  • i = 1，窗口内没有元素，输出 0
  • 第 2~m 项，窗口左边界是 1，无需判断队头是否出窗（因为 j=i-1 ≤m-1 <m，窗口大小不足 m，不会有元素超出左边界）。

注意，由于题目是要求，求每一项前的 m 个数到它这个区间内的最小值，所以说

  • 先处理第 j项（j 从 1 到 n），再输出第 j+1 项的答案

分析给出的样例，n=6，m=2，数列 a=[7,8,1,4,3,2]

  1. i=1：输出 0 → 处理 j=1（a [1]=7）→deque=[1]；
  2. i=2：窗口 [1,1]（j=1）→ 队头 1≥1 → 输出 a [1]=7 → 处理 j=2（a [2]=8）→ 队尾 7<8 → 入队→deque=[1,2]；
  3. i=3：窗口 [1,2]（j=1、2）→ 队头 1≥max (1,3-2)=1 → 输出 a [1]=7→ 处理j=3（a [3]=1）→ 队尾 8>1 删 2，队尾 7>1 删 1 → 入队→deque=[3]；
  4. i=4：窗口 [2,3]（j=2、3）→ 左边界 max (1,4-2)=2 → 队头 3≥2 → 输出 a [3]=1 → 处理 j=4（a [4]=4）→ 队尾 1<4 → 入队→deque=[3,4]；
  5. i=5：窗口 [3,4]（j=3、4）→ 左边界max (1,5-2)=3 → 队头 3≥3 → 输出 a [3]=1 → 处理 j=5（a [5]=3）→ 队尾 4>3 删 4 → 队尾 1<3 → 入队→deque=[3,5]；
  6. i=6：窗口 [4,5]（j=4、5）→ 左边界 max (1,6-2)=4 → 队头3<4 → 出队→deque=[5] → 输出a [5]=3→ 处理 j=6（a [6]=2）→ 队尾 3>2 删 5 → 入队→deque=[6]；

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.StringTokenizer;

class FastReader {
    BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    StringTokenizer st = new StringTokenizer("");

    String next() {
        while (!st.hasMoreTokens()) {
            try {
                st = new StringTokenizer(br.readLine());
            } catch (IOException e) {
                e.printStackTrace();
            }
        }
        return st.nextToken();
    }

    int nextInt() {
        return Integer.parseInt(next());
    }
}

public class Main {
    public static void main(String[] args) throws IOException {
        FastReader sc = new FastReader();
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

        int n = sc.nextInt();
        int m = sc.nextInt();
        int[] a = new int[n + 1];
        for (int i = 1; i <= n; i++) {
            a[i] = sc.nextInt();
        }

        int[] queue = new int[n + 2];
        int h = 1, t = 0;

        bw.write("0\n");

        // 处理j=1到n-1（因为i从2到n，对应j=i-1）
        for(int j = 1; j < n; j++) {
            // 1. 维护单调递增队列：删除队尾比当前元素大的下标
            while(h <= t && a[queue[t]] >= a[j]){
                t--;
            }

            // 2. 当前元素下标入队
            queue[++t] = j;

            // 3. 窗口左边界：i = j+1，左边界 = max(1, (j+1)-m) = j+1 -m（若j+1-m >=1）
            int left = (j + 1) - m;
            // 只有左边界>1时，才可能有元素超出窗口
            if (left > 1){
                if(queue[h] < left){
                    h++;
                }
            }

            // 4. 输出第i=j+1项的答案（队头是窗口最小值）
            bw.write(a[queue[h]] + "\n");
        }

        bw.flush();
        bw.close();
    }
}

image-20251117211149438